La boucle à verrouillage de phase
Nous verrons en fin de ce chapitre plusieurs utilisations de la boucle à verrouillage de phase, mais commençons par l'utilisation la plus courante, qui est de stabiliser un oscillateur (VCO) en comparant sa fréquence à
celle d'un oscillateur de référence. Nous piloterons donc un Oscillateur à fréquence variable
(VCO) grâce à une boucle qui l’asservit à une fréquence de référence «Fin».
Le comparateur de phase sort une tension ( continue quand l'asservissement fonctionne): La valeur de cette tension sera telle que le VCO oscille sur la fréquence voulue.
La fréquence de référence Fin est issue d'un oscillateur de grande stabilité, généralement piloté par un quartz... Dans le schéma ci-dessous, la fréquence du VCO est divisée par N, de façon à la comparer à la fréquence de référence.
Le VCO sera ainsi stabilisé sur une fréquence Fout = N fin
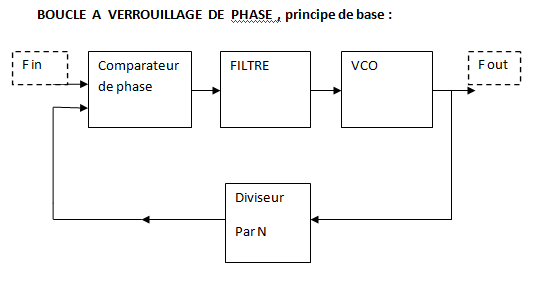
Un schéma classique d’une boucle de verrouillage de phase est donc celui-ci :
Un mot sur le diviseur de fréquence...
On trouve des diviseurs de fréquences fixes divisant souvent par une puissance de deux, et des diviseurs de fréquence programmables....
Les progrès technologiques permettent de diviser les fréquences de plus en plus hautes. On trouve facilement des diviseurs de fréquences fonctionnant même en bande Ku.. Mais dans des circuits hybrides, on trouve des diviseurs intégrés fonctionnant bien au delà. Cela signifie qu'aujourd'hui, on sait réaliser des sources de fréquences stables sur tout le spectre de fréquences utilisées....
Un mot sur le comparateur de phase....
Un comparateur de phase classique est ;constitué par multiplication des deux signaux d'entrée. La sortie donne une tension continue fonction de l'écart de phase : il faut que les deux signaux soient en quadrature pour que la tension continue varie en plus ou en moins autour de sa valeur centrale.
Mais avec un tel comparateur, lorsque l'écart de fréquence est important, la tension de sortie ne reflète plus la phase et la boucle ne se verrouillera pas.....
Il existe depuis longtemps des comparateurs de phase qui peuvent être assimilés aussi à des comparateurs de fréquence: la tension de sortie filtrée reste ;à zéro ou à un si les deux signaux ont des fréquences trop différentes. Le circuit le plus utilisé est le très connu CD 4046 et ses successeurs. C'est la sortie "tristate" de ce circuit que nous utiliserons dans l'exemple que nous donnons plus loin.
Détermination du filtre et Fonction de Transfert
Comme tous les systèmes asservis, la stabilité de la boucle de phase va dépendre de la fonction de transfert en boucle ouverte.
Différents filtres et fonctions de transfert sont possibles.
Pour déterminer le filtre, nous allons utiliser la méthode du diagramme de Bode, qui a l'avantage de nécessiter peu de calculs et de montrer ce qui se passe.
Pour étudier cette stabilité, il est nécessaire de définir certains termes:
Kv : pente du VCO en radians/V.
Si le VCO a une pente p (en Hertz par volts), alors Kv = 2π.p
Kφ : sensibilité de sortie du comparateur
de phase, en volts par radians. Par exemple, avec un comparateur de phase du type cmos "tristate" comme le CD 4046, on a :
Kφ = Vdd / 4π
N = rang de division de la sortie du VCO.
La boucle ouverte, sans filtre, a une réponse du 1er ordre. Elle est représentée en noir dans le graphe de Bode ci-dessous.
ωo est la pulsation à laquelle la réponse de la boucle ouverte sans filtre coupe l'axe 0 dB
On a ωo= Kφ.Kv / N
Ce paramètre ωo dépend donc du comparateur de phase et du VCO, il est donc en général prédéterminé. Il est important de le connaître avant de décider du filtre qui sera placé derrière le comparateur de phase.
La boucle sera stable si la courbe de réponse en boucle ouverte est moins pentue que -12dB/octave au point ou la courbe coupe l'axe horizontal 0 dB du diagramme de Bode. (Cette condition de pente est équivalente à la condition : phase supérieure à -180° Critère de Revers).
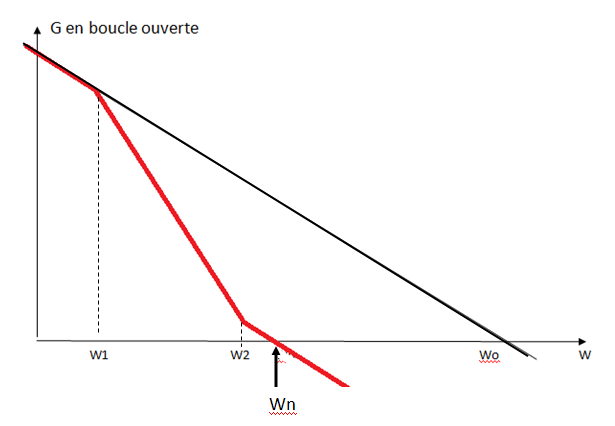
On voit que sans filtre, la pente de la courbe en noir sera au pire de -6dB/octave, donc la boucle sera toujours stable...
Maintenant rajoutons un filtre entre la sortie du comparateur de phase et l'entré du VCO.
Premier cas, si le filtre rajouté ne présente pas de fréquence de coupure en dessous de ωo, la boucle sera inconditionnellement stable, car dans ce cas, la courbe de réponse en boucle ouverte a une pente de l'ordre de −6 dB par octave jusqu'à ωo.
C'est le cas de figure des boucles PLL pour les démodulateurs, et pour les cas où le bruit généré par le comparateur n'ont pas une importance essentielle.
Deuxième cas, si le filtre rajouté présente une fréquence de coupure en dessous de ωo. C'est généralement le cas des synthétiseurs de radio fréquences, et des boucles très lentes de récupération de la porteuse. Mais alors attention, ; la boucle peut être instable..
Nous devons dans ce cas considérer avec soin la nouvelle courbe en boucle ouverte ( en rouge) ;:
Supposons donc que le comparateur de phase est suivi d'un filtre passe bas du premier ordre, de pulsation de coupure ω1,
inférieure à ωo.
La boucle ouverte est alors un système du second ordre. Au delà de ω1 le diagramme de Bode montre une pente qui se rapproche des 12 dB par octave.
Pour avoir un système stable, il faut que la pente de la courbe n'atteigne pas −12 dB par octave au point ωn où la courbe rouge coupe l'axe horizontal "0 dB".
On créer pour cela un deuxième coude dans la fonction de transfert, à la pulsation ω2, pour "redresser" la courbe et la ramener à une pente ;plus faible que −12 dB par octave au point où la courbe coupe l'axe 0 dB.
En tenant compte du filtre avec ω1 et ω2, la pulsation à laquelle la boucle ouverte a un gain 0 dB est nommée ωn, c'est la "fréquence naturelle de la boucle".
La stabilité peut s'évaluer par le facteur d'amortissement ksi : On considère que le verrouillage s'effectue le plus rapidement possible pour ksi = 0,7. Dans ce cas, on a une montée stable de la tension de sortie du filtre.
Les valeurs plus faibles de ksi induisent des sur-oscillations importantes, voire permanentes, et pour les valeurs de ksi plus grande que 1, il n'y a plus de sur-oscillations, mais l'état stationnaire est atteint plus lentement.
La stabilité peut aussi s'évaluer par la marge de phase : à la fréquence ωn, c'est l'écart de phase par rapport à la phase qui entraînerait une instabilité.
Réduction du bruit issu du comparateur de phase : On rajoute en général derrière le filtrage cité ci-dessus, une autre cellule qui coupe à une fréquence ω3. Cette fréquence ω3 doit être au moins 7 fois supérieure à ωn, et supérieure à ωo ;pour ne pas réduire la stabilité obtenus précédemment.
EXEMPLE DE CONSTITUTION DU FILTRE DE BOUCLE EN SORTIE D' UN COMPARATEUR "TRISTATE"
Le filtre ci-dessous FIG 145 est constitué de R1, R2 et C2
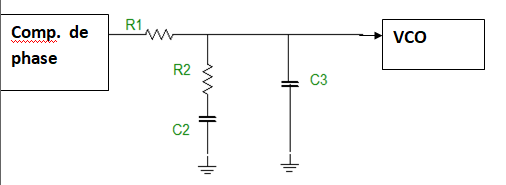
On a ici: ω1 = 1/((R1+R2).C2) et ω2 = 1/(R2.C2)
On a calculé précédemment ωo qui dépend des caractéristiques du VCO, du comparateur, du rang de division ...
ωo= Kφ.Kv / N
On se donne alors ωn en tenant compte des critères suivants:
Plus ωn sera grand, plus le verrouillage sera rapide.
En contre partie, le filtrage des résidus et bruits issus du comparateur de phase sera mauvais.On optera en général pour un ωn assez inférieur à ωo pour cette raison.
Connaissant ωo et ωn, on en déduira
ω1 = ωn2/ωo
On en déduit alors (R1 +R2) et C2 sachant que
les résistances font quelques milliers d'ohms.
Le calcul de R2 se fera après avoir choisi le coefficient d' amortissement ksi :
On choisira ksi compris entre 0,7 et 1 ;
on a alors R2=(1/C2).((2ksi/ωn)-(1/ωo))
Remarque: en général on trouve que R2 est deux à 5 fois plus petite que R1.
Rajout d'une coupure à ω3 :
Afin de réduire encore le bruit, on a intérêt à rajouter une nouvelle coupure à ω3.
Un condensateur C3 sera placé en parallèle sur la sortie du filtre. Donc la valeur de C3 sera de l'ordre de 1/(R2.ω3)
Pour ne pas nuire à la stabilité, on prendra en pratique ω3 bien supérieur à ωn, par exemple ω3 = 7 ωn
Exemple numérique :
- Soit un VCO oscillant à F = 512 MHz
- avec une pente p = 20 MHz/Volt
- le comparateur de phase est un CD4046 sous VDD = 9 Volts. On utilise la sortie PC2, phase comparator tri-state, le plus intéressant.
- les canaux sont espacés de ;50 KHz ;donc on divise F par N = 10240 de façon que les fréquences appliquées au comparateur soient égales à l'espacement des canaux : 512 MHz /10240 = 50 KHz
Calcul du filtre à rajouter :
Kφ = VDD / 4π = 9V / 4π = 0,716
Kv = 2π.p = 6.28 x 20 106 = 125.106
Donc : ωo = Kφ.Kv / N = 0,716 x 125.106/10240 = 8740rd/s
Choisissons maintenant ωn = 1000 rd/s
Donc : ω1 = ωn2 / ωo = 10002 / 8740 = 114 rd/s
ω1 = 1/ ( R1 + R2).C2
Choisissons C2 = 1µF
R1 + R2 = 1/ω1.C2 = 1 / 114.10-6 = 8800Ω
Choisissons ksi = 0.7
R2 = (1/C2).((2ksi/ωn)-(1/ωo)) = 1300Ω
Donc R1 = 8800 - 1300 = 7500 Ω
En choisissant C2 = 1 µF.
Comme ce n'est pas très critique, on prendra : R1 = 8200 Ω et R2 = 1200 Ω
Stabilité et bruit de phase
Le signal de sortie du VCO est sensé être stable en fréquence. En effet, sa fréquence est directement proportionnelle à celle de la référence.
Oui, mais les dérives éventuelles du VCO ne seront « rattrapées » que si ces variations ne sont pas trop rapides. En effet, la boucle n’est pas infiniment rapide et le signal de correction appliqué au VCO est limité en fréquence.
En pratique, les variations de fréquences plus rapides que Fn = ωn/2π ne seront pas corrigées.
Donc :
- On pourra moduler en fréquence le VCO par des fréquences supérieures à ωn /2π.
- Les dérives «lentes» du VCO seront corrigées.
- Si on veut moduler en fréquence le VCO par des fréquences très basses (inférieures à Fn), il faudra moduler la référence. Ce sera aussi le cas si on module par des signaux numériques qui présentent une composante continue non nulle sur un temps long.
Bruit de phase :
Tout signal issu d’un oscillateur possède une modulation de phase parasite (On peut aussi considérer que ce signal est modulé en fréquence par la dérivée du signal modulant en phase…)Cette modulation parasite est en général constituée par un bruit blanc et est gênante :
- Apparition de bandes latérales de bruit sur le spectre,
- Dégradation du rapport S/B de la modulation FM,
- Utilisé en oscillateur local, réduction de la sélectivité sur les voix adjacentes pour les récepteurs bande étroite ;à grande sélectivité.
Le bruit de phase du VCO dépend de plusieurs facteurs, notamment:
- le coefficient de surtension du circuit LC,
- le facteur de bruit du transistor oscillateur,
- le niveau d’oscillation (il ne le faut pas trop faible pour rester loin du bruit du transistor) ;
- et même la tension de bruit thermique de la résistance qui attaque les varicaps, si la pente est très grande et si on cherche des bruits de phase très bas…
La référence de fréquence, elle, est généralement un oscillateur à quartz, et donc, du fait du Q du quartz, possède un bruit de phase très inférieur à celui du VCO.
Donc, la boucle de phase va réduire le bruit de phase du VCO concernant les fréquences inférieures à Fn = ωn/2π. Le bruit présent dans spectre du VCO va donc être amélioré autour de la porteuse, jusqu’à une distance ωn/2π de la porteuse.
Sur la figure ci-dessous,la courbe 1 montre le bruit de phase du VCO non verrouillé, la courbe 2 montre la réduction du bruit autour de la porteuse, grâce à la boucle de phase. La courbe 3 montre le bruit de phase résiduel du à la référencence, en général bien plus faible.
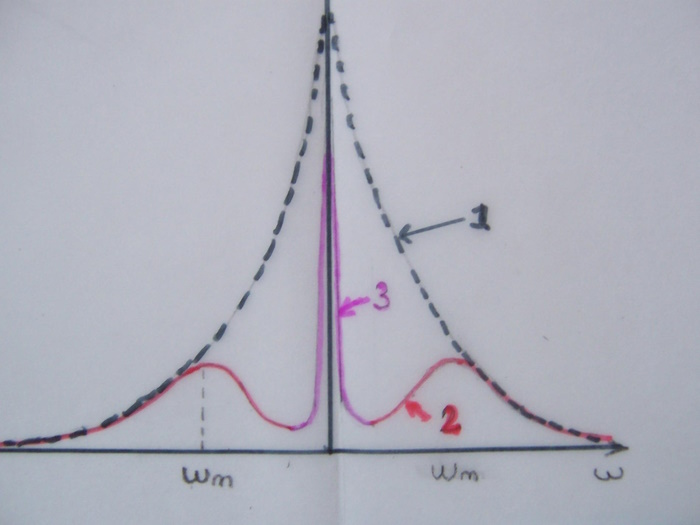
On peut chercher à réduire le bruit de phase à une distance plus grande de la porteuse. C'est notamment le cas en
hyperfréquences.
Par exemple, des vibrations mécaniques pourront moduler le VCO en fréquence et se superposer
à la modulation. Il faudra donc un ωn plus élevé.... donc on est limité par ωo ;
→ Il faudra donc augmenter Kφ, Kn ou diminuer N.
;Mais là aussi, dans la zone "verrouillée", on se heurtera à une limite, c'est le bruit ramené par les éléments de la boucle : bruit de l'AOP, bruit thermique de résistances, bruit de la source de référence...
Utilisation des boucles à verrouillage de phase
L'utilisation la plus courante, c'est celle que nous venons de voir : stabiliser un oscillateur (VCO) en comparant la fréquence à celle d'un oscillateur de référence. Mais il y a d'autres utilisations :
Démodulateur de fréquence ou de phase.
Si nous choisissons ωn suffisamment élevé, la boucle va imposer au VCO les variations rapides de la référence. Si nous remplaçons la référence de fréquence par le signal FM ou φM à démoduler, le VCO sera modulé de la même façon que le signal à démoduler par sa tension de commande.
Le signal Fm démodulé est donc présent sur la tension de commande. La boucle ;à verrouillage de phase sera donc ici un démodulateur de fréquences.
On peut montrer que ce type de démodulateur est un peu meilleur que les discriminateurs de fréquence classiques, lorsque le rapport signal / bruit est très bas.
Sa linéarité sera celle de la caractéristique ;tension/ fréquence de la tension de commande.
Le circuit CD4046 ou ses versions plus rapides est souvent utilisé. On utilisera alors l'un des deux comparateurs de phase disponibles (pas forcément le "tri-state"), ainsi que le VCO intégré. La pente du VCO sera fonction de la fenêtre de fré quence qu'on aura choisie.
Récupération de la porteuse :
Nous avons vu, au chapitre sur les mélangeurs RF, le démodulateur à quadrature qui permet de démoduler quasiment tous les types de modulation reçues par un récepteur, en fournissant les signaux i et q caractéristiques de la modulation traitée. Mais très souvent, le démodulateur à quadrature exige de disposer de la fréquence exacte, voire la phase, de la porteuse du signal à démoduler.
Parfois, le spectre du signal reçu présente des traces de la porteuse, ce qui permet de régénérer celle-ci par filtrage spectral. Mais si on ne peut récupérer la porteuse à l'aide du spectre du signal reçu, une solution sera la boucle de verrouillage de phase...
Récupération de la porteuse d'un signal modulé en phase ou en fréquence :
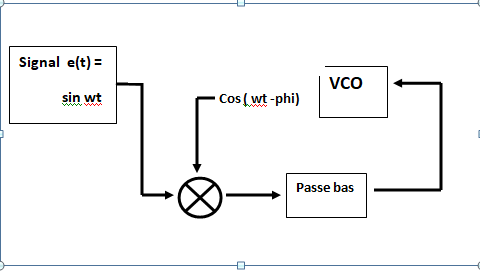
Le schéma ci-dessous montre une boucle de phase très classique, avec un multiplieur utilisé pour comparer la phase. On entre sur le comparateur de phase :
- le signal d'entrée : sin ωt
- un signal issu du VCO. Pour comparer les phases avec ce type de comparateur, il faut que les signaux soient proches de la quadrature, aussi nous désignons par cos (ωt + φ) ;le signal du VCO.
Quand la boucle est verrouillée: φ = 0 et la tension continue appliquée au VCO maintient son signal en quadrature avec le signal d'entrée.
Supposons maintenant que le signal d'entrée soit modulé en fréquence ou en phase. Si la phase du VCO ne bouge pas, la sortie du comparateur de phase ne sera plus une tension continue, mais reflètera les variations de phase du signal d'entrée. Si le filtre passe bas coupe toutes les fréquences de modulation, la tension appliquée au VCO ;sera fonction de la différence de phase moyenne . La fréquence du VCO restera verrouillée sur la fréquence moyenne du signal d'entrée.
Notons que si le signal d'entrée est modulé en AM, le principe reste le même à condition que l'amplitude de la porteuse ne soit jamais nulle.
Récupération de la porteuse d'un signal DSB, ;
la boucle de Costas pour récupérer la porteuse.
Qu'est-ce qu'un signal DSB (double side band ) ?
C'est un signal obtenu à l’émission par multiplication d’une «porteuse» sin (ωt) par un signal
modulant quelconque m(t).
e(t) = m(t). sin (ωt)
Ce type de signal obtenu par multiplication directe est souvent utilisé pour des émissions numériques...
Le signal de modulation m(t) peut prendre des valeurs positives, et négatives (contrairement à l'AM où m(t) reste positif).
La boucle de phase décrite précédemment ne fonctionne plus pour la raison suivante :
Quand m(t) passe d'une valeur positive à une valeur négative, la phase instantanée du signal ;m(t) sin (ωt) s'inverse,
passant de zéro à 180 degrés. La sortie du comparateur de phase ne réalise plus un feedback négatif.
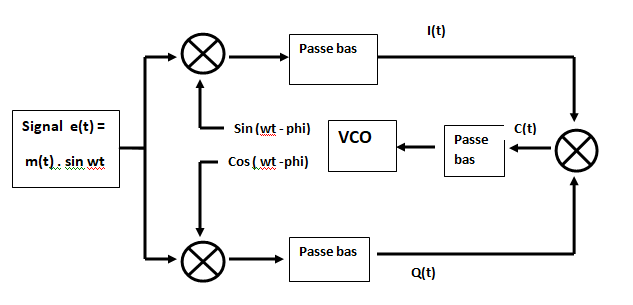
Mise en oeuvre de la boucle de Costas pour la DSB:
Nous appliquons à deux multiplieurs le signal reçu e(t) = m(t) sin wt
Supposons que notre VCO puisse osciller sur cette fréquence porteuse. Mais pour l’instant, il a une phase quelconque φ.
Notre but, c’est de faire osciller ce VCO en phase avec la porteuse. (φ = 0)
La sortie du VCO sin (wt-φ) est appliquée
sur le multiplieur du haut.
Sa sortie déphasée de π/2 : cos (ωt - φ), est appliquée sur le multiplieur du
bas.
La sortie du multiplieur du haut est :
m (t) sin ωt.sin (ωt-φ) = ½ m(t) [cos (ωt – ωt+φ) – cos (2ωt-φ)]
car sin a sin b = ½ [ cos (a-b) - cos ( a+b) ]
À la sortie du filtre passe bas, le terme souligné est éliminé. Il reste donc :
i(t) = ½ m(t) cos (φ)
La sortie du multiplieur du bas est :
m(t) sin ωt. cos (ωwt - φ) = ½ m(t) [sin (2wt - φ) + sin (φ)]
Le terme souligné est éliminé par le passe bas, et il reste donc :
q (t) = ½ m(t) sin (φ)
Le troisième multiplieu r fait le produit i.q, ce qui donne :
i.q = ¼ mcarré(t) cos (φ) sin (φ) = (1/8) m2 sin (2φ).
Cette sortie c(t) filtrée est appliquée
sur la commande du VCO.
Le Vco sera verrouillé quand cette sortie sera nulle (φ = 0)
Remarque importante : pourquoi cette boucle fonctionne contrairement à la boucle de phase classique ?
Avec la boucle de Costas, le terme qui multiplie sin 2φ est un carré donc toujours positif. Il n'y a pas saut de phase de 180° quand le signal m(t) passe d'une valeur positive à une valeur négative.
Remarquons que i(t) permet de retrouver la modulation en amplitude.
Cependant, la boucle de Costas peut présenter quelques difficultés.
- si m(t) s’annule, le signal est nul pendant un instant… Il faudra que le VCO fonctionne "en roue libre" pour ne pas perdre la phase. (grâce au filtrage passe bas)
- On voit aussi que le verrouillage peut avoir lieu si φ = 180°, car "2φ" donne un déphasage nul
La boucle de Costas peut récupérer ;la porteuses d’autres signaux plus complexes qu’un signal DSB. Par exemple BPSK,....Dans ce cas, le signal d'entrée ne sera pas simplement m(t) sin ωt, et la boucle sera plus complexe.
Nous avons donné la procédure avec des multiplieurs analogiques, mais évidemment, toutes ces fonctions peuvent être réalisées par des circuits ;numériques.