Les lignes de transmission
Vous trouverez dans ce chapitre des informations sur les lignes de transmission, mais aussi sur des fonctions qui les utilisent : résonateurs, transformateurs, coupleurs.Les lignes de transmission, c’est quoi ?
Le problème :
En radiocomunications, comment transporter un signal RF d’un générateur (ou source) jusqu’à une «charge» R (ou «récepteur») à une certaine distance ?
On reliera le générateur à la charge par une "ligne de transmission", qui sera par exemple un câble coaxial, ou, sur une carte, une piste avec sa masse en dessous, etc...

Si on connecte en bout de cette ligne une résistance de charge "R", la question qui se pose, c’est de savoir quelle impédance sera vue par le générateur à l’autre extrémité.
La question est à priori légitime, puisqu’une piste présente une inductance et une capacité parasites.
Eh bien, pour une fois, la nature fait bien les choses. En effet, si on choisit convenablement les paramètres physiques de la ligne de transmission,
la ligne reproduira à son extrémité la résistance R qu’on a connectée en bout.
Et cela, quelle que soit sa longueur. On dit alors que la ligne a une "impédance caractéristique Zc" égale à R.

Note : Pour les fréquences UHF qui nous occupent ici, nous parlerons "des lignes de transmission TEM", comportant donc deux conducteurs.
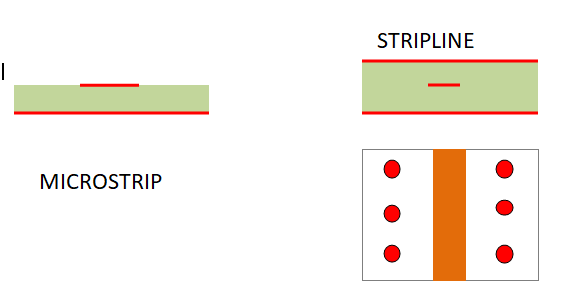
La ligne de transmission peut être une piste sur une carte, évoluant au dessus d’un plan de masse. Ce qu’on nomme "microstrip".
Si W est sa largeur, et si h est sa hauteur au dessus de la masse, pour un isolant donné, le rapport W/h définira l’impédance caractéristique de cette ligne.
Par exemple, si la charge R en bout de la piste est égale à 50Ω, la piste (ligne), devra avoir "une impédance caractéristique" de 50Ω. Elle présentera alors cette résistance à son autre extrémité.
Pour une carte dont l’isolant est l’époxy, Une impédance caractéristique de 50Ω est obtenue si W/h = 1,85, où W est la largeur de la piste et h l’épaisseur de l’époxy entre piste et plan de masse.

La ligne de transmission peut être aussi un câble coaxial qui transportera de la même façon, le signal de la source jusqu’à la charge.
Les rapports des diamètres du conducteur central et du blindage du câble sont choisis pour que son impédance caractéristique soit en général 50Ω.
Presque toujours, les appareils RF des laboratoires présentent des résistances d’entrée et des résistances de sortie de 50Ω. Pour relier ces appareils entre eux, on doit donc utiliser des câbles coaxiaux d’impédance caractéristique 50Ω. (câble RG58CU).
Ainsi, les équipements verront toujours 50Ω.
ligne symétrique ou asymétrique.
Pour les fréquences UHF, la plupart des lignes de transmission d’aujourd’hui sont des câbles coaxiaux pour les transports de signaux extérieurs aux équipements, ou des pistes imprimées pour le transport des signaux sur une carte.
Toutes ces lignes sont composées d’un conducteur associé à une masse qui le suit partout.
Mais pour les fréquences plus basses, on peut trouver aussi des lignes symétriques composées de deux conducteurs identiques, ce sont les lignes "bifilaires", d’impédance caractéristique souvent de 300 Ω qui sont très peu utilisées de nos jours.
Enfin, pour les fréquences plus hautes, aux hyperfréquences, on trouvera des guides d’ondes, (mais qui ne sont plus en mode TEM. Nous n’en parlerons pas ici)
Ondes stationnaires
Et si ces conditions ne sont pas remplies ?Les ondes stationnaires.
Si le câble "d’impédance caractéristique Zc = 50Ω" est connecté en bout à une charge différente de 50Ω, l’impédance que la ligne présentera à son autre extrémité dépendra alors de sa longueur.
La tension RF ne sera pas la même partout sur la ligne, et le courant non plus.
On peut interpréter ce phénomène en considérant le signal le long de la ligne comme une "onde":
Si la ligne n’est pas chargée à son extrémité par son impédance caractéristique, une partie de l’onde qui arrive sur la charge va être réfléchie et repartir dans l’autre sens. En certains endroits, l’onde réfléchie sera en phase avec l’onde incidente, et en d’autres endroits elle sera en opposition.
Prenons un exemple :
J’envoie sur un câble (Zc =50Ω) qui n’a pas de pertes, un signal RF sinusoïdal de puissance 1 watt. Si le câble est chargé en bout par 50Ω, alors on a vu qu’il présentait de mon côtéune résistance de 50Ω quelle que soit sa longueur. Je dois donc appliquer une tension de 7 volts eff, puisque P = V2/R
Supposons maintenant que la charge en bout du câble soit 150Ω. Dans ce cas, le tableau plus bas nous dit que 25 % de la puissance qui arrive sur la charge de 150Ω va être "réfléchie" et va repartir dans l’autre sens.
Si 1 watt correspond à 7 volts, alors 0,25 watt correspond à 3,5 Volts.
à certains endroits du câble, la tension de l’onde directe et la tension de l’onde réfléchie s’ajoutent : on aura 7 + 3,5 = 10,5 V
à d’autres endroits, elles sont en opposition et se retranchent : 7V - 3,5 V = 3,5 V
Donc il n’y aura pas partout dans le câble la même tension ni le même courant. On montre que les maxima sont distants de λ/2, ainsi que les minima.
On appelle ROS (Rapport d’ondes stationnaires) le rapport entre les tensions maximales et les tension minimales.
Dans notre exemple, ce sera 10,5 / 3,5 = 3
Remarquez que le ROS est le rapport entre la résistance qu’il y a en bout (150Ω), et celle qu’il aurait fallu pour être adapté (50Ω). Mais pour faire ce rapport, on fait toujours le rapport entre la plus grande et la plus petite, de façon que le rapport soit supérieur à 1.
Voici un tableau indiquant quelques valeurs à connaître, pour un câble "50Ω" :
| Résistance de charge | Puissance réfléchie | ROS |
|---|---|---|
| 50Ω | 0% | 1 |
| 100Ω ou 25Ω | 11% | 2 |
| 150Ω ou 16,5Ω | 25% | 3 |
| OΩ ou ∞ | 100% | ∞ |
Bien sur, l’idéal c’est d’avoir une onde progressive, soit un ROS de 1. Dans cette situation, toute la puissance que fournit le câble est absorbée par la charge.
Des appareils très courants, les ROS mètres ou réflectomètres, permettent de mesurer la puissance directe et la puissance réfléchie en un endroit du câble. Vous trouverez au chapitre sur les mesures le détail de cette mesure.
Pertes d’une ligne de transmission
Comme rien n’est parfait en ce monde, un câble coaxial introduit des pertes, par effet joule, par pertes diélectriques, etc.
Les pertes d’un câble coaxial seront d’autant plus élevées que son diamètre sera réduit, que la fréquence sera élevée et que sa longueur sera grande.
La qualité de l’isolant jouera aussi un role.
Le constructeur du câble donne ces pertes, fonctions de la fréquence.
Ainsi, à 100 MHz, un câble RG58 (le plus courant, qu’on trouve partout dans les labos) présentera par exemple 15 dB de pertes pour 100 mètres. Si on a 20 mètres de câble,
on aura 3dB de pertes (les pertes en dB sont proportionnelles à la longueur, ce qui est bien commode).
Donc si j’applique un watt à ce câble, il n’arrivera que 0,5 W soit la moitié de la puissance, à l’extrémité (-3dB).
Remarquez le piège si je mesure le taux de puissance réfléchie d’une antenne vue au bout d’un long câble :
Supposons que ma charge soit une antenne, mais, manque de chance, celle-ci est coupée (Z = l’infini).
Toute la puissance sera réfléchie et repartira vers la source. Mais en parcourant le câble, la puissance qui revient sera à nouveau divisée par deux. Donc côté source, j’enverrai 1 watt, et je ne verrai revenir que 0,25 W. Je pourrai croire que mon antenne n’est pas si mauvaise que cela, alors qu’en fait elle est coupée !!
Conséquence : Si on veut mesurer le taux de puissance réfléchie par une antenne, il faudra tenir compte des pertes dans le câble, entre le point de mesure et l’antenne, si ces pertes ne sont pas négligeables.
Les pertes d’un câble augmentent avec la fréquence. Pour le câble RG58CU, et pour une longueur de 100 mètres, on a environ:
à 100 MHz : 15 dB
à 500 MHz : 65 dB
à 1 GHz: 100 dB
Réaliser une ligne d’impédance caractéristique donnée sur le circuit imprimé ;
Je veux réaliser une ligne d’impédance caractéristique donnée, sur mon circuit imprimé. Cette piste doit être impérativement au dessus du plan de masse, et celui-ci sans coupure. Bien sur, cette masse doit être reliée à la source d'un côté et à la charge de l'autre... Si W est la largeur de la ligne, et si h est la hauteur au dessus de la masse (h est donc l’épaisseur de l’isolant), des courbes qu’on trouve facilement donnent l’impédance caractéristique fonction de W/h, pour un substrat donné.
Par exemple, pour un isolant époxy FR4, on a les valeurs suivantes d’impédance caractéristique :
| W/h | 0,3 | 0,5 | 0,7 | 1 | 2 | 4 |
| Zc (Ω) | 100 | 85 | 75 | 65 | 48 | 30 |
Dans certains cas rares, on place la piste entre deux plans de masse. On n’a plus affaire à un "microstrip" mais à une "stripline" ou "triplaque".
Le stripline permet de réduire légèrement la place et permet un blindage total au rayonnement.
Si on conserve les mêmes distances entre la piste et les plans de masse, il faudra réduire environ de moitié la largeur W de la piste pour conserver une impédance caractéristique de 50Ω.
Mais il faudra aussi réunir de part et d’autre les deux plans de masse par un alignement de vias, le long de la ligne. (figure ci-dessous).
Le coefficient de vélocité d’une ligne de transmission :
L’onde se propage dans une ligne moins vite que dans le vide, notamment si il y a un isolant (diélectrique) autre que l’air.
La longueur d’onde dans la ligne sera alors plus courte.
Il faudra multiplier la longueur d’onde dans le vide (λ0 = C/F) par un coefficient de "vélocité" k.
On obtiendra ainsi la longueur d’onde dans la ligne, que je note toujours "λG".
λG = k.λ0
Pour un câble coaxial RG58 dont l’isolant est du polyéthylène, le coefficient de vélocité est k = 0,66.
Pour un coaxial à isolant téflon (PTFE), k = 0,7
Pour une ligne imprimée microstrip avec un W/h donnant Zc = 50 ohms :
- Sur substrat époxy FR4 : W/h = 1,85 et k = 0,49 à 0,55
- Sur substrat téflon : W/h = 2,7 et k = 0,64
- Sur substrat alumine : W/h = 1,0 et k = 0,35
Impédance présentée par la ligne de transmission si l’autre extrémité n’est pas chargée par l’impédance caractéristique ?
Nous allons voir d’abord deux cas particuliers importants :
La ligne "demi-onde" :
Une ligne demi-onde répète à son extrémité l’impédance qu’on lui a placée à l’autre extrémité. En d’autres termes, la ligne demi-onde ne change pas l’impédance, même si son impédance caractéristique n'est pas celle de la charge.
Mais c’est quoi, une ligne demi-onde ? Vous allez dire, facile ! Connaissant la fréquence, je calcule la longueur d’onde λ = C / F. Ainsi, avec F = 300 MHz, j’aurai λ = 1 mètre.
Oui, mais voilà, ceci n’est vrai que si l’isolant de la ligne est du vide ou de l’air. Or, la plupart du temps, l’isolant d’un câble, ou l’isolant d’une piste, ce n’est pas de l’air, et il faudra appliquer le coefficient de vélocité. Donc
la ligne sera plus courte.
Finalement, quelle sera la longueur d’une ligne demi-onde à 300 MHz, pour du câble RG58CU ?
Pour ce câble, le coefficient de vélocité est k = 0,66. Donc ce sera la demi-onde dans le vide : 0,5 m mais multiplié par 0,66 donc 33 cm.
La ligne "quart d’onde" :
Si la longueur de la ligne est égale à un quart d’onde, alors la ligne "inverse" l’impédance : si il y a un court circuit à l’extrémité, ou trouve un circuit ouvert à l’autre extrémité.
Et inversement, si elle est ouverte, on trouve un court circuit à l’autre bout.
D’une façon générale, soit une ligne quart d’onde d’impédance caractéristique ZC. Si on place une résistance R1 en bout, on trouve une résistance R2 à l’autre bout, telles que
R1.R2 = Zc2.
Par exemple, un câble coaxial 50Ω de longueur quart d’onde, chargé par R1 = 10Ω, montrera à son autre extrémité: R2 = 250Ω.
Bien sur, là aussi il faudra tenir compte du coefficient de vélocité k.
Et si la longueur de ma ligne est quelconque ?
Il est possible, grâce à l’abaque de Smith, de connaître l’impédance qu’on voit à l’extrémité d’une ligne de longueur L, connaissant l’impédance caractéristique de cette ligne, le facteur de vélocité k, et l’impédance qui est connectée à son autre extrémité. On calculera d’abord la longueur d’onde dans la ligne (λG): c’est la longueur d’onde dans le vide (λ zéro) multipliée par k . Un tour complet correspond à une demi-onde : 0,5 λG. D’ailleurs, le cercle extérieur de l’abaque n’est pas gradué en degrés, mais directement en "λG" . En particulier, si on tourne d’une demi-onde, (tour complet) on retrouve le même point, ce qui est normal, on vient de voir qu’une demi-onde ne changeait pas l’impédance.....
Exemple sur l’abaque de Smith
L’abaque de Smith va nous permettre de trouver l’impédance présentée par une ligne, connaissant l’impédance présente à l’autre extrémité.
Le constructeur donne l’impédance d’entrée d’un circuit intégré : Z = 100 – j 60Ω.
Sur une carte epoxy, une piste de longueur 35 mm arrive sur ce circuit. Cette piste a une largeur de 1,5 mm et est à la distance de 0,8 mm du plan de masse.
Quelle impédance trouve-t-on à l’extrémité de cette piste, à F = 1 Ghz ?
- On a donc W /h = 1,5 /0,8 = 1,87 Pour ce rapport, sur époxy, l’impédance caractéristique de la ligne est Zc = 50Ω.
- On calcule la longueur d’onde dans le vide "λ zéro" = C/F = 30 cm
En tenant compte du facteur k = 0,5 de l’époxy,la longueur d’onde sur la ligne est "λG" = k.λ zéro = 0,5.30 cm = 15 cm = 150mm. - On prend "λG » comme unité : cette piste mesure donc : 35mm /150mm = 0,23 fois «λG»
- On prend l’impédance caractéristique comme unité: l’impédance, appelée "réduite" , du circuit intégré est donc :
z = 100 /50 - j 60/50 = 2 – 1,2 j - Considérons l’abaque de Smith en "impédance réduite". (Cela signifie que le centre montre une résistance de "1" ).
Sur l’abaque de Smith: Nous tra&çons le point A : 2- 1,2 j :
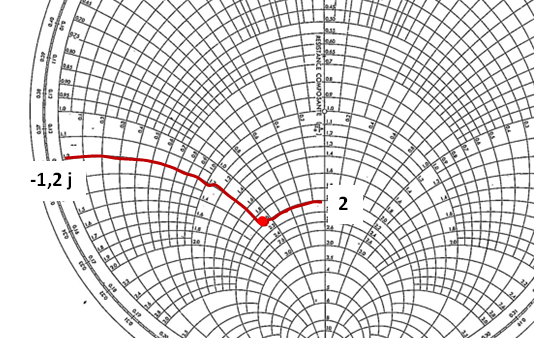
Puis nous tournons de 0,23 fois « λG » dans le sens des aiguilles d’une montre. Pour cela, on peut s’aider du cercle gradué extérieur de l’abaque, gradué en λG, sachant que 1 tour complet correspond à 0,5 « λ G ».
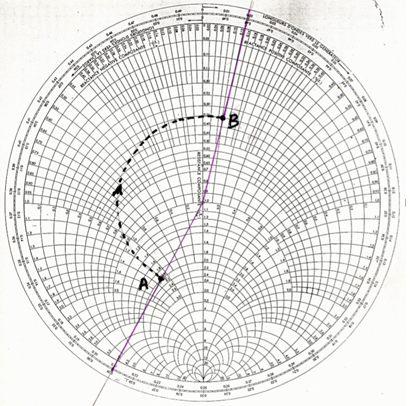
- On obtient ainsi le point B :
on lit l’impédance réduite, en suivant les lignes de l’abaque : z = 0,35 + 0,1 j. - On en déduit l’impédance en Ω à l’extrémité de cette piste, en multipliant l’impédance réduite par 50 : 0,35 . 50 + j 0,1.50 = 17,5 Ω + j 5 Ω
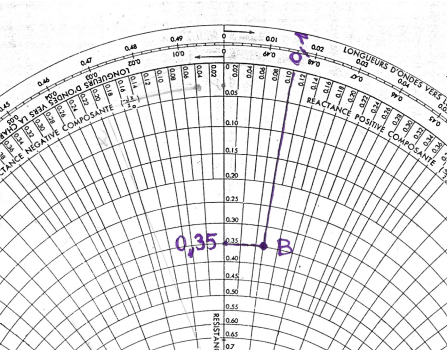
Dans quel sens tourner sur l’abaque de Smith ?
Lorsque l’abaque de Smith sert à trouver l’impédance x que nous montre la ligne, chargée par une impédance Z à l’autre extrémité, on part du point Z et on tourne dans le sens des aiguilles d’une montre pour trouver le point X :
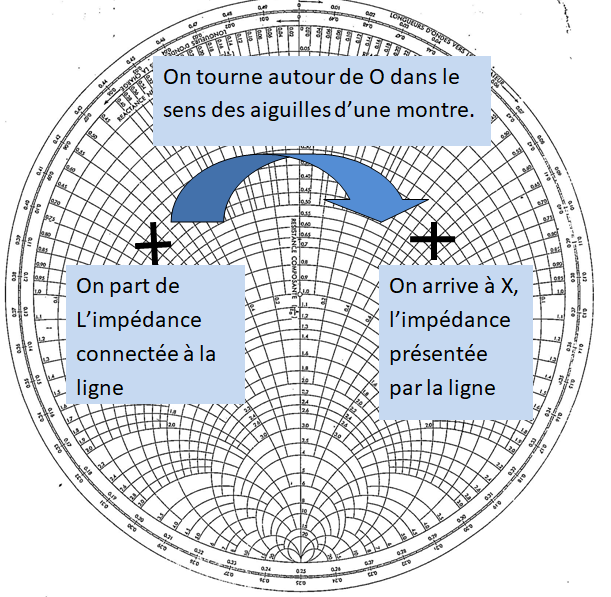
Remarque 1 : l’impédance X, c’est celle qu’on voit, celle présentée par la ligne.
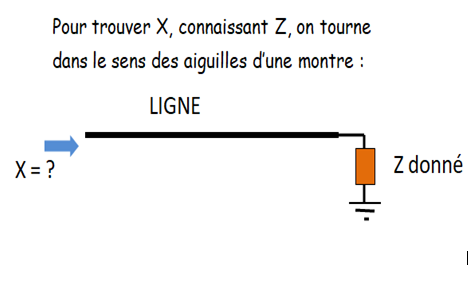
Remarque 2 : On tourne en sens inverse des aiguilles d’une montre quand on connaît l’impédance présentée par la ligne, et qu’on cherche l’impédance qui est connectée à l’autre extrémité.
Par exemple, pour trouver l’impédance d’une antenne quand on a accès à l’extrémité du câble coaxial. Ce sens de rotation est à éviter dans tous les autres cas si on n’a pas l’habitude de l’abaque, car il fait faire souvent des erreurs.
Vous remarquerez que cette méthode ne fait pas intervenir où se trouve le "générateur". On simulera un générateur simplement en rajoutant la source de tension.
Autre exemple :
Inductance d’un morceau de piste court-circuitée à la masse.
Que voit-on à l’extrémité d’une piste courte dont l’autre extrémité est en court-circuit ?
Soit une piste d’impédance caractéristique 50Ω sur époxy (k = 0,55), de longueur 15 mm, mise à la masse à son extrémité. Nous sommes en 430 MHz.
A 430 MHz, λ0 = 70 cm.
λG = k.70 cm = 0,55.70 = 38,5 cm.
Une piste de 1,5 cm fait donc en unité λG :
1,5cm / 38,5 cm = 0,04 λG
Sur l’abaque de Smith, nous partons du point correspondant à un court circuit : Z = 0Ω
donc Z réduite = 0/50 = 0
Nous tournons de 0,04 λG, nous obtenons un point d’impédance réduite : + 0,26 j
Nous passons en Ω en multipliant par 50Ω : 0,26j x 50 = +j13 Ω
à 430 MHz, une impédance de +j13 Ω, c’est une self de 5 nH, qui va à la masse.

On voit que l’abaque de Smith permet de trouver l’inductance d’une piste courte qui va à la masse. On pourrait de la même façon, en partant d’un circuit ouvert, trouver la capacité de petits morceaux de pistes "en l’air", en partant de Z = l’infini.
Ces pistes ont des valeurs de selfs ou de capas qui ne dépendent pas de la fréquence tant que leur longueur est très courte devant le quart d’onde. Dans l’exemple ci-dessus, on aurait pu prendre une autre fréquence , plus basse, on aurait trouvé encore environ 5 nH.
D’une façon générale :
- Un morceau de ligne court (càd inférieur au quart d’onde) mis à la masse se comporte comme une inductance.
- Un morceau de ligne court et en l’air se comporte comme un condensateur.
- Une ligne quart d’onde à la masse à son extrémité, c’est un circuit ouvert.
- Une ligne quart d’onde ouverte à son extrémité, c’est un court-circuit...
Faire la différence entre le coefficient de réflexion S11 et l’impédance..
On a vu que lorsqu’une ligne arrive sur une charge, une partie de la puissance apportée par la ligne va repartir (se réfléchir) si la charge n’est pas égale à l’impédance caractéristique de la ligne.
Le coefficient de réflexion S11 indique l’amplitude et le déphasage du signal qui "repart". ( On considère le champ électrique de l'onde qui repart, donc l'onde repart en phase pour une charge infinie , puisque E est alors maximum.)
Souvent, il est nécessaire de convertir le coefficient de réflexion en impédance.
Par exemple, les fabricants de transistors indiquent le coefficient de réflexion S11 de l’entrée du transistor....
Ils sous entendent que la ligne en question a une impédance caractéristique de 50Ω, ce qui signifie qu’une longueur "1" sur l’abaque correspond à 50Ω. On dit que l’abaque est normalisé à 50Ω. On obtient les impédances réduites en divisant par 50.
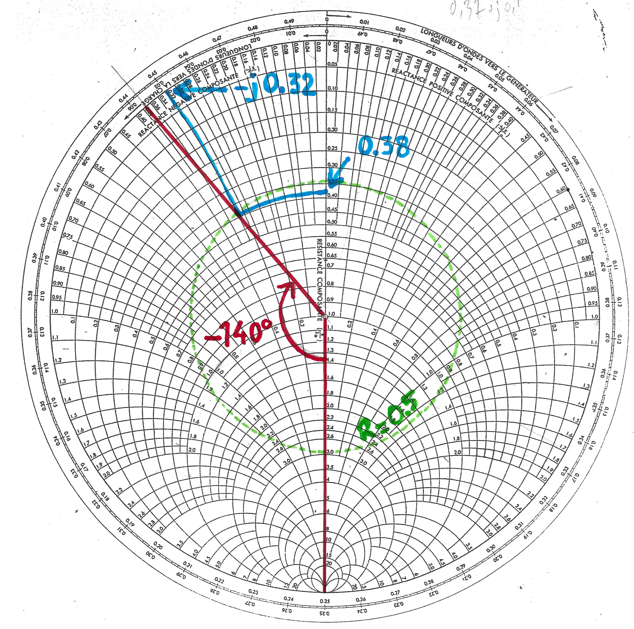
Prenons un exemple : Soit un coefficient de réflexion de la charge S11 = 0,5/-140 degrés.
Cherchons quelle est l’impédance de cette charge.
Rappelons que l’abaque de Smith "en impédance réduite" a un rayon est égal à 1.
On trace alors un cercle central de rayon r = 0,5 et on note le point d’angle -140 degrés.
Sur ce point, en suivant les lignes de l’abaque, on trouve :
la partie réelle de l’impédance : 0,38 et la partie imaginaire : - j 0,32
Donc l’impédance réduite z = 0,38 – j 0,32
L’abaque était normalisé à 50Ω, donc pour avoir les impédances en Ω, on multiplie par 50.
Z in = 0,38.50 – j 0,32.50 = 19Ω – j 16Ω.
Ruptures d’impédance :
Il peut arriver que localement, on ne respecte pas l’impédance caractéristique d’une ligne.
Par exemple, une capacité supplémentaire peut être involontairement introduite en parallèle quelque part sur la ligne et provoquera une rupture d’impédance :
On veillera à ce qu’aucune autre masse ne soit présente très près de la piste, sinon la capacité entre la piste et la masse sera trop grande.
On se méfiera par exemple des pastilles, ou des connecteurs en bout de cette piste, si la masse du connecteur est côté piste.
Il est parfois nécessaire de réduire localement la largeur de la piste. Il manquera donc là un peu de capacité.
Mais si la longueur de la piste ainsi amincie est inférieure à 1% de λ, l’abaque de Smith montre que la perturbation est négligeable.
Lors de l’entrée ou de la sortie d’un composant ou d’un module quelconque, il faudra aussi toujours s’intéresser au courant de retour, qui passe dans la masse, et qui doit rester sous la ligne, sans s’en écarter, sinon on aura là aussi une rupture d’impédance.
Le (Routage et CEM des cartes radio) donne des exemples d’erreurs d’implantation.
Rupture d’impédance sur une ligne longue.
Un problème courant de ligne de transmission consiste à rechercher où se trouve une rupture d’impédance sur un câble coaxial long. Vous trouverez, au chapitre sur les mesures en RF et CEM cette mesure à l’aide d’un analyseur vectoriel (VNA).
Profitons en pour faire quelques remarques sur l’adaptation :
On sait que le transfert de puissance sera maximum, (on dit qu’on est "adapté") quand la résistance de la source est égale à la résistance de la charge. C’est ce qu’on tente de faire, en RF, et cette résistance, est en général de 50Ω.
Mais il arrive que la source ou la charge présentent une impédance avec une partie "réactive" (imaginaire).
Pour réaliser l’adaptation, il faudra alors que la charge et la source présentent des impédances dites "conjuguées",
c’est à dire de parties imaginaires opposées.
Par exemple, si une charge présente une impédance de 40Ω + j 70Ω, alors l’impédance de la source devra être 40Ω - j 70Ω.
Si la charge en bout de ligne de transmission n’est pas une résistance pure, on ne pourra pas trouver un ROS de 1.
Si on laisse la large telle qu’elle est, on pourra toujours adapter à la source ce qu’on trouve à l’extrémité de la ligne.
Mais la ligne ne fonctionnera plus en onde progressive, sa longueur ne sera plus quelconque, et les pertes augmenteront.
faut-il toujours adapter ?
En RF, on a généralement intérêt à adapter la charge à la ligne de transmission, car on a intérêt à connaître l’impédance que la source voit, à l’autre extrémité de la ligne.
Si la ligne est adaptée côté charge (de 50Ω, par exemple), la source qui voit cette ligne, "voit" une résistance de 50Ω, quelle que soit la longueur de la ligne.
Une question se pose : Cette source doit-elle nécessairement présenter elle aussi une résistance de sortie de 50Ω ?
Si la puissance fournie par cette source est "chère" à obtenir (par exemple une antenne de réception), il faut adapter pour que cette source fournisse toute la puissance qu’elle est capable de fournir.

En théorie, il n’est pas toujours indispensable d’adapter la source à la ligne. En effet, il suffit que la charge soit adaptée à la ligne pour qu’il n’y ait pas d’ondes stationnaires. Si on a une source à très basse impédance de sortie, le fait de lui connecter la ligne 50Ω changera peu sa tension de sortie. Dans ce cas, la source donne à la ligne une puissance constante P = Vcarré /50Ω. (C'est le cas de votre ligne 220 volts...)
Dans le cas d’un signal numérique de transmission de données, si on a une charge désadaptée, une réflexion sur la source du signal réfléchi va provoquer un aller-retour du signal sur la ligne, ce qui provoquera des interférences inter symboles.
Donc en général, on adapte aussi la source à la ligne...
Un autre cas qu'il faut signaler, c'est si la source et la charge sont très proches , inférieures à 0,5% de lambda: On peut les réunir directement sans passer par une "ligne" . Il suffit de vérifier que l'inductance ou la capacité du conducteur qui les relie a une influence négligeable sur le signal...C'est parfois le cas des fréquences très basses, ou de l'audiofréquence
Le rayonnement d’une piste :
Il passe dans la masse, sous la piste, le même courant que dans la piste, mais de sens opposé, que j’appelle parfois "courant de retour". Ces deux courants sont normalement très proches, et induisent donc dans l’espace loin de la piste des champs opposés. Pour cette raison, la piste rayonne très peu dès qu’on s’en éloigne.
Champ proche : Un point M de l’espace proche de la piste ne sera pas tout à fait à la même distance du courant de la piste et du courant dans la masse. Donc les champs en M dus au courant de la piste et dus au courant dans la masse ne seront pas tout à fait égaux à cause de cette différence de distance. Mais lorsqu’on s’éloigne de la piste, les distances deviennent presque égales, et ces champs, opposés, deviennent presque égaux.
Leur résultante devient donc de plus en plus petite : le rayonnement de la piste s’estompe.
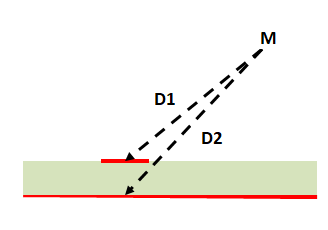
champ lointain : On a supposé ci-dessus que les champs étaient exactement opposés. Mais cet écart des distances donne aussi un déphasage, qui sera d’autant plus grand que la longueur d’onde est courte. Donc les champs dus au courant dans la piste et dus au courant dans la masse ne s’annuleront pas tout à fait, car ils ne seront plus parfaitement opposés.
Ce déphasage persistera même si on s’éloigne. Donc aux fréquences élevées, le rayonnement d’une piste va décroître moins vite qu’Aux fréquences basses ; On dit que la piste rayonne un champ électromagnétique.
Nous avons raisonné avec les courants (champs magnétiques) mais le raisonnement sera le même avec les tensions (champs électriques).
Donc, c’est un principe fondamental, pour réduire le rayonnement d’une piste il faut que les courants «aller» (dans la piste) et «retour» (dans la masse) soient les plus rapprochés possible….Et cela d’autant plus que la fréquence est élevée.
D’où la catastrophe d’une fente dans le plan de masse : Il est important de ne pas couper la masse sous la piste.
En effet, Si on coupe la masse, le courant sous la piste va devoir s’éloigner de la piste pour reboucler son circuit. La piste devient alors une antenne !
Nous verrons d’ailleurs que pour réaliser une antenne, il faut par tous les moyens éloigner le courant dans un conducteur du courant.
Courrant de gaine d'un câble coaxial
Dans un câble coaxial transmettant un signal, il circule un courant sur le conducteur intérieur, l’âme du câble. Mais il circule aussi le courant de retour à la surface intérieure du blindage, égal au courant de l’âme, mais de sens opposé. Cela peut surprendre, mais en haute fréquence, ce courant du blindage ne passe pas normalement sur la surface extérieure du câble. Notons que les courants internes du câble ne sont pas influencés par le "monde" extérieur au câble, quoi qu’on fasse au câble: l’enrouler, l’entourer de ferrite, etc.
Cependant,en pratique,le blindage d’un câble n’est jamais parfait, notamment si on veut des isolations importantes, que ce soit dans le sens "émissions parasites" vers l'extérieur du câble , ou pour les "perturbations issues de l'environnement".
Ainsi, une partie du courant sensé circuler à l'intérieur peut se retrouver sur la surface extérieure du blindage. Ce courant est dit "courant de gaine" ou " de mode commun" .
Ce courant de gaine peut apparaître si le blindage du câble n'est pas parfait. De ce point de vue, les câbles à double tresse et les câbles semi-rigides sont meilleurs que les câbles à tresse unique. Il faut en tenir compte si on veut par exemple une isolation supérieure 80 dB entre deux câbles qui se cottoient...
Mais ce courant de gaine pourra aussi apparaître si les connexions d'extrémités sont mal conçues:
Notamment, un courant de gaine important pourra apparaître si le câble coaxial est connecté à une antenne symétrique.
Il apparaîtra aussi quand la connexion de masse d'une transition n'est pas assez courte .
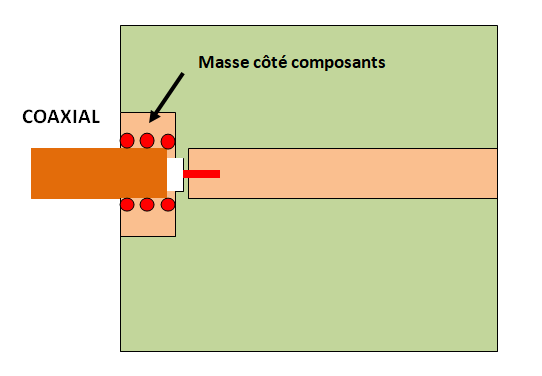
Par exemple, il arrive parfois que la sortie RF d’une carte doive être soudée à un câble coaxial. Il faut connecter la masse du câble à la masse de la carte, le plus près possible sous la piste , afin que le courant de masse ne fasse pas de détour et s’éloigne de la piste … La tresse de masse du câble devra être la plus courte.
La figure ci-contre montre ce qu’il ne faut pas faire, une connexion de masse trop longue !

Pour éviter de créer une liaison de masse trop longue, on plaquera et on soudera la masse du câble sur la masse de la carte. Si le câble n’est pas soudé côté plan de masse, on fera remonter une masse côté composants avec suffisamment de vias, comme indiqué.
Blocage du courant de gaine :
Le courant de gaine pose toujours des problèmes, et il faudra toujours essayer de l'éviter. On peut par exemple réduire le courant de gaine en enfilant un tube de ferrite sur le câble, au plus près de la connexion. Ce tube présentera une impédance grande au courant de gaine, mais ne sera pas « vu » par les courants intérieurs.
D'une façon générale, il ne faudra jamais connecter une ligne symétrique ( bifilaire) à une ligne asymétrique ( coaxial ou piste) sans introduire un symétriseur"....Le tube ferrite en est un.
Découplage hyperfréquence par ligne quart d'onde.
Les lignes de transmission peuvent être utilisées pour d’autres fonctions que le transport d’un signal:Pour isoler, découpler : les stubs quart d’onde.
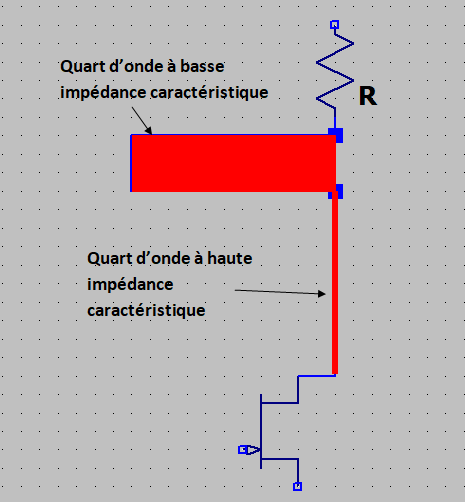
On a vu qu’une ligne de longueur quart d’onde ouverte présente un court circuit à son extrémité, et réciproquement, une ligne quart d’onde fermée présente un circuit ouvert à son autre extrémité. L’association d’un stub quart d’onde série à haute impédance et d’un stub quart d’onde parallèle à basse impédance permet d’amener l’alimentation ou une polarisation sur un transistor sans que celui-ci ne voit l’impédance de cette polarisation.
Exemple d’alimentation d’un transistor en hyperfréquences :
Sur la fréquence pour laquelle on a des "quart d’onde", le stub large présente un court circuit au niveau de la résistance. Mais ce court circuit est transformé en circuit ouvert vu par le transistor, grâce à la seconde ligne quart d’onde.
Les stubs d’adaptation :
De courts tron&çons de lignes, placés en parallèle sur une ligne principale peuvent se comporter comme des capacités ou des inductances en parallèle sur cette ligne, à la fréquence considérée, et permettent de réaliser des transformation d’impédance.
Pour connaître la valeur de la capacité ou de la self présentée par un tel "stub", on utilise l’abaque de Smith.
Par exemple, un stub de longueur inférieure à un quart d’onde, et ouvert à son extrémité est vu comme un condensateur, d’autant plus grand qu’on se rapproche du quart d’onde.
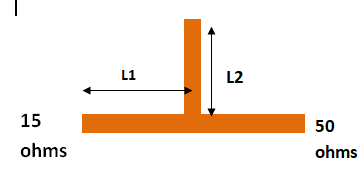
Exemple :
une adaptation « simple stub » qui transforme 15Ω en 50Ω grâce à un stub de longueur L2 placé
à la distance L1 de la résistance de 15Ω. Toutes les lignes ont Zc = 50Ω
Solution:
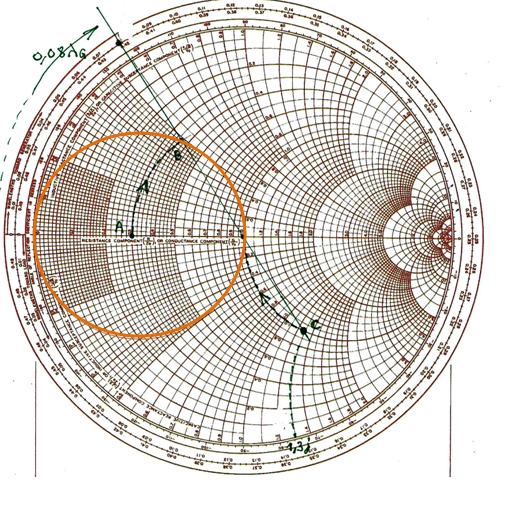
Nous raisonnons sur l’abaque de Smith normalisé à 50Ω ci-dessous :
Tra&çons d’abord le cercle orange, symétrique par rapport au centre, du cercle R = 1.
On part de R = 15Ω, soit une impédance réduite r = 15/50 = 0,3
On place donc le point A (r = 0,3) sur l’abaque
Pour arriver au point B sur le cercle orange, on voit qu’il faut tourner de 0,08 λG autour du centre.
Donc L1 = 0,08 λG
Maintenant, on veut rajouter quelque chose en parallèle, donc il faut "passer en admittance". Pour cela, on prend le point symétrique de B ⇛ point C
Pour arriver au centre, d’admittance 1, on doit donc rajouter une admittance de +1,3j.
On "repasse ensuite en impédance", mais le point est déjà au centre, donc on reste là. L’impédance sera aussi de 1, c’est-à-dire 50Ω, c’est ce qu’on voulait.
Maintenant, comment créer une admittance de +1,3 j à l’aide du stub L2 ?
(une admittance positive imaginaire, c’est une capacité....).
On part de l’extrémité ouverte du stub, donc on part d’une admittance nulle : point D de l’abaque en mode admittance.
Pour atteindre le point E d’admittance 1,3 j, il faut tourner de 0,145λG.
Donc L2 = 0,145 λG
En résumé :
L1 = 0,08 λG.
L2 = 0,145 λG.

Remarque, pour définir ce stub L2, si vous voulez rester à vous balader sur l’abaque en "mode impédance" :
Une admittance de +1,3 j, c’est une impédance z = 1/1,3j = -0,77j
Vous partez d’une impédance infinie (le stub est ouvert au bout), et vous tournez jusqu’au point d’impédance -0,77j.
Pour y arriver, vous avez tourné de (graduation extérieure)
0,395 - 0,25 λG = 0,145 λG

Nous n’avons pas encore parlé de fréquence ....
Supposons que nous soyons sur époxy 8/10, et à F = 1,5 GHz :
Largeur de la piste :
Pour Zc= 50Ω, w/h = 1,85 donc
w = 1,85x h = 1,85 . 0,8 = 1,5 mm
Longueur d’onde dans le vide λ= C/F = 20 cm.
Coefficient de vélocité d’une ligne époxy 50Ω : k = 0,55
λG = 20 cm x 0,55 = 11cm
Donc :
L2 = 0,145 λG = 16 mm
L1 = 0,08 λG = 8 mm
Les lignes résonantes :
Une longueur de ligne de transmission peut être utilisée comme résonateur, et se comportera de façon analogue à un circui LC. Rappelons que λG est égale à λ dans le vide multiplié par le coefficient de vélocité k de la ligne considérée.
Ligne demi-onde fermée : une longueur D de piste à la masse aux deux extrémités constitue un résonateur à λG/2. Le point chaud est au centre.
Ligne quart d’onde : Une ligne à la masse à une extrémité et ouverte à l’autre constitue un résonateur λG/4. Le point chaud sera situé coté ouvert.
Ligne demi-onde ouverte : une ligne ouverte aux deux extrémités constitue aussi un résonateur à λG/2. Il y a un point chaud aux extrémités, et un ventre de courant au centre.
Les lignes résonantes occupent une place importante sur les fréquences UHF, en dessous du GHz. On trouve dans le commerce des lignes quart d'onde avec un isolant céramique de constantec diélectrique de 80...Ce qui réduit de presque dix fois la longueur. Ces "résonateurs dielectrique TEM" permettent la réalisation de filtres de bande stables et sans condensateur d'accord . Vous trouverez un exemple dans le chapitre "Circuits couplés" .
Résonateurs couplés :
On peut évidemment réaliser des filtres de bande en couplant correctement des lignes résonantes (demi-onde ou quart d’onde).
Les règles sont les mêmes que pour les circuits LC couplés. Par exemple, si l’apparition d’un creux dans la bande passante sur le couplage entre résonateur est trop important. (voir le chapitre "couplage de circuits résonant").
exemple: un filtre en bande X constitué de deux résonateurs demi-onde couplés.

Si la longueur d’onde est plus longue, les résonateurs (lignes λ/2) sont assez encombrants.
Une solution consiste à utiliser une ligne quart d’onde (mise à la masse côté froid).
Une autre solution consiste à replier la ligne demi-onde en forme de U. Ci-dessous un fitre 2,4 GHz, de bande passante quelques MHz, sur un circuit strip-line d’épaisseur 16/10, et d’epsilon 3,4. Le pas est de 1,27 mm, les lignes d’entrée et sortie sont bien sur en 50Ω.

A noter :
- Le sens du couplage entre les lignes d’entrée et le résonateur est tel que les extrémités en l’air soient opposées, sinon le couplage en champ E et le couplage en champ H se contrarient.
- Même chose pour le sens des lignes, il faut qu’elles soient "tête-bêche" pour que le couplage en champ E et le couplage en champ H s’additionnent.
Lors de la mise au point d’un filtre à deux résonateurs couplés, on déterminera, dans l’ordre :
- La distance entre les lignes de couplage d’entrée / sortie et les résonateurs, qui donne le Qc des résonateurs.
- La distance entre les deux résonateurs, qui donne le couplage, donc la forme de la courbe de réponse : couplage critique, surcouplage, etc...
Le couplage entre lignes dépend non seulement de la distance entre elles, mais aussi de la distance à la masse (épaisseur du substrat).
Comme le couplage dépend de plusieurs paramètres, il est commode de simuler de tels filtres par un logiciel électromagnétique 3D.
Utilisation des lignes quart d'onde à constante diélectrique élevée
Dans les bandes UHF , pour avoir une bonne reproductibilité d'un filtre de bande, on peut remplacer les circuits LC par des lignes dites "résonateurs diélectriques TEM".
Un inconvénient des lignes, c'est la place ...Mais ce problème est résolu en utilisant des résonateurs diélectrique quart d'onde à fort epsilon , que l'on trouve dans le commerce. Aini, un résonateur quart d'onde autour du GHz , avec epsilon = 40, aura une longueur réduite à 1 cm environ...
Ces résonateurs diélectrique sont très intéressants pour réaliser des filtres de bande entre 300 MHz et 3 Ghz...Ils ne nécessitent pas d'éléments de réglage et sont très stables.
Voici un exemple ci-dessous de filtre 950 MHz , de bande passante 20 MHz, sans réglage, sur plan de masse. Le schéma et la simulation sont sous SPICE. Vous trouverez aussi un exemple d'implantation, grille au pas de 1.27mm.
Nous avons couplé par capas en tête deux résonateurs quart d'onde 1 Ghz qui remplacent les circuits LC parallèle.
Les résonateurs de fréquence 1 GHz utilisés ici ont une impédance caractéristique de 8 ohms, et sont simulés par des lignes de Td = T/4 = 0,25 nS. Les capas C4 et C5 représentent la capacité des pads des soudures.
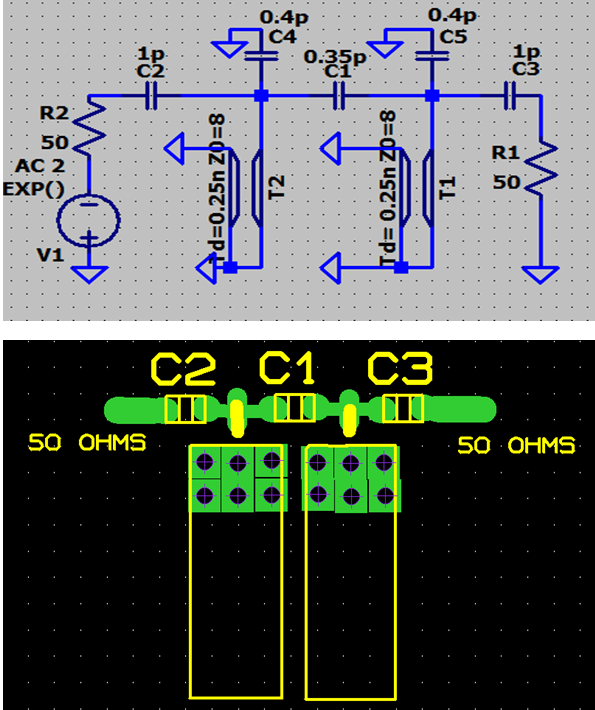
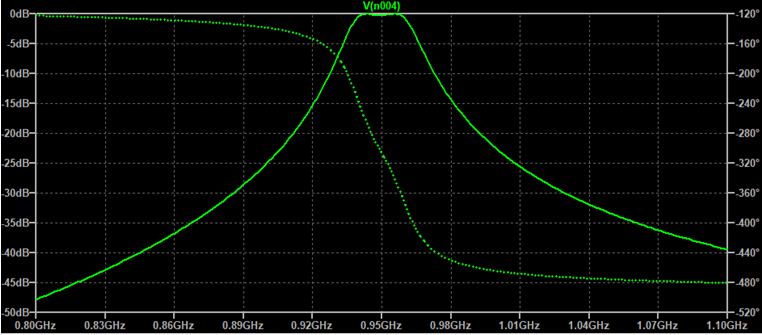
Voici la courbe de réponse . Attention, à cause des lignes , nous aurons aussi une réponse vers 2500 MHz, la fréquence triple. Pour éviter cette réponse, on fera suivre le filtre d'un petit circuit en pi passe bas de coupure vers 1 GHz.
Modifier la fréquence d’un résonateur à lignes.
Très souvent, pour les résonateurs à Q élevé, il est délicat de tomber très exactement sur la fréquence désirée.
On pourra modifier légèrement la fréquence de résonance de plusieurs façons.
Par exemple, pour un résonateur demi-onde ouvert aux extrémités :
- On augmente la fréquence en enlevant un peu de cuivre sur le point chaud, c’est à dire sur les extrémités libres. (on diminue la capacité en ce point)
- On diminue la fréquence en réalisant une fente qui "pince" la ligne sur un ventre de courant, c’est à dire au centre de la ligne. (on augmente l’inductance en ce point). Ou bien, en collant un peu de cuivre sur les points chauds.
Résonateur quart d’onde raccourci.
Ce résonateur est constitué d’une ligne quart d’onde dont une extrémité est à la masse, et l’autre extrémité "ouverte".
On peut réduire encore la longueur en plaçant une capacité terminale.
Par exemple, pour réduire la longueur de moitié, (donc λ/8) avec une ligne d’impédance caractéristique 50Ω,
il faudra une capacité terminale d’impédance -j50Ω. (facile à vérifier avec l’abaque de Smith).
En général, on constitue ainsi des résonateurs à Q élevé, donc la capacité doit être suffisamment précise pour être ajustée.
Voyez le dessin.
A la résonance, si on applique une résistance en un point, on trouvera une autre résistance sur un autre point.
la ligne est raccourcie au moins de moitié par le condensateur, la résistance présentée par la ligne sera proportionnelle au carré de la distance à la masse. Sans toutefois descendre en dessous de la résistance "série" de la ligne.

Prenons un exemple :
Sur un substrat téflon, à 430 MHz nous voulons transformer une résistance de 2000Ω en 50Ω à l’aide d’une ligne résonante raccourcie à 5 cm, d’impédance caractéristique 70 Ω.
λ zéro est donc de 70 cm
Pour le téflon, k = 0,65 donc λG = 0,65.70 = 45 cm
calculons la capacité d’accord:
En partant du court-circuit à la masse, à gauche, et en remontant de L=5 cm, nous remontons donc de L/λG = 5/45 = 0,11 λG
Sur le diagramme de Smith, en partant de Z = 0, nous tournons de 0,11 λG, et nous trouvons sur le cercle : z = j 0,83, soit en Ω : 0,83.Zc = 0,83.70 = +j58Ω
La ligne présente donc une impédance de +j58Ω à 50 mm du court-circuit. Pour accorder la self de cette ligne, il faudra un condensateur de -j 58Ω, soit à 430 MHz : C = 6,3 pF
Nous connectons maintenant la résistance de 2000Ω au sommet, sur le condensateur.
Nous cherchons en quel point il faut se connecter pour trouver 50Ω:
Le rapport des résistances est de 2000/50 = 40, donc le rapport des longueurs est sa racine carrée, soit 6,3.
Le point à 50Ω sera donc à 50mm/6,3 = 8mm de la masse.
Ce calcul est approché, et nous avons négligé les pertes propres de la ligne.
Coefficient de surtension Qo d’un résonateur à lignes ;
>Le coefficient de surtension Qo à vide de ces résonateurs va dépendre des pertes de la ligne utilisée.
Ces pertes seront dues :
- Aux pertes diélectrique du substrat. L’époxy sera moins bon que le téflon, lequel sera moins bon que l’alumine ou l’air.
- A la résistance ohmique de la ligne.
- Au rayonnement, d’autant plus important que la ligne est éloignée de la masse.
Au delà du GHz, l’époxy possède beaucoup de pertes (Qo de l’ordre de 50 au mieux)
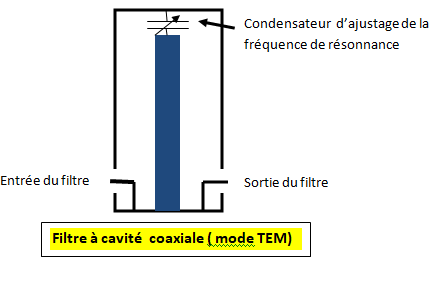
Pour avoir un Qo maximum, plutôt que des lignes imprimées, on utilisera des lignes coaxiales avec diélectrique air :
On réalise des cavités résonnantes à très fort Q en plaçant un conducteur central dans un cylindre.
La figure montre la coupe d’une telle cavité dite "TEM". Il existe dans la littérature technique des abaques donnant le meilleur rapport des diamètres pour des pertes minimales. On atteint ainsi des Qo dépassant le millier....
Comme on raccourcit la ligne à l’aide d’une capacité terminale, il faudra être très vigilant sur la résistance série de ce condensateur, pour ne pas dégrader le Qo.
Attention aux résonances parasites sur une carte !
En fait, sur une carte, on peut créer sans le vouloir des résonateurs qui peuvent poser des problèmes. Par exemple, deux condensateurs de découplage qui découplent une piste d’alimentation et distants d’une distance D, créent un résonateur sur la fréquence pour laquelle D est la demi-onde.
Cela peut poser des problèmes sur une carte, que nous aborderons dans le chapitre "Routage et CEM des cartes radio"
La ligne transformateur d’impédance.
Soit une ligne quart d’onde d’impédance caractéristique Zc.
on charge son extrémité » par une résistance R1, on trouvera à l’autre extrémité de la ligne quart d’onde une résistance R2 telles que R1.R2 = carré de Zc.
Par exemple, si cette ligne d’impédance ZC = 75Ω est chargée par 50Ω, on trouvera 112Ω à l’autre extrémité.
Une ligne quart d’onde ouverte se comportera donc comme un court circuit à son autre extrémité..
Une ligne quart d’onde ouverte pourra donc réaliser un découplage, méthode très utilisée en hyperfréquences. Bien sur, le découplage ne sera effectif que dans une bande de fréquence.
Cependant, les lignes sont souvent encombrantes pour les fréquences inférieures au GHz. Pour cette raison, lorsque la place est un paramètre important, on réalisera les transformateurs d’impédances et les filtres par des composants L et C localisés. (voir le chapitre sur les adaptations par circuit LC )
Lignes utilisées en coupleur
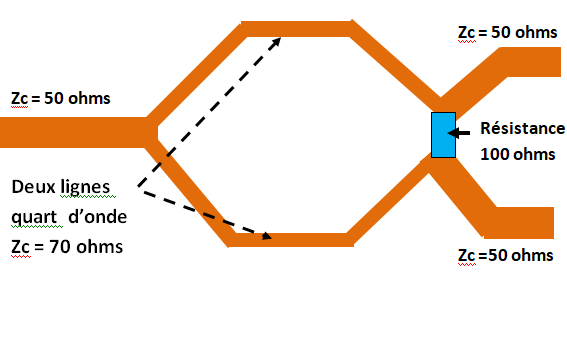
Le Coupleur de Wilkinson
Ci-contre un coupleur de Wilkinson avec lignes imprimées. Chaque ligne quart d’onde (λG/4) ayant Zc = 70Ω, transforme en 100Ω le signal de chaque entrée 50Ω.
Les deux lignes de sortie 100Ω sont mises en parallèle pour retrouver 50Ω sur la sortie simple. ( à gauche sur le dessin )
Le coupleur de Wilkinson est un coupleur «3dB en phase».
Si on applique à son entrée simple un signal de puissance P, on retrouvera sur ses deux sorties jumelles un signal P/2, chacun sous 50Ω et en phase.
Réciproquement, si on applique sur chaque entrée jumelle un signal, on retrouvera la somme de ces signaux sur sa sortie simple.
Attention, ici deux cas possibles :
1er cas : Les deux signaux appliqués sont identiques, (même fréquence et en phase)
Dans ce cas, la sortie simple nous donne la somme des deux puissances, (puisque la résistance R a la même tension sur ses deux bornes, elle ne dissipe rien).
Exemples d’applications : Couplage de deux antennes en phase. Les signaux sont identiques, on récupère en réception la somme des signaux de chaque antenne, d’où un gain de « 3dB » , et en émission, on répartit symétriquement la puissance sur les deux antennes.
Autre exemple: Coupler deux émetteurs de même fréquence , on obtient la somme des puissances.
2ème cas : Les deux signaux appliqués sur les entrées jumelles ont des fréquences différentes :
Dans ce cas, la sortie simple nous donne la somme des deux signaux, mais chacun atténué de 3dB. Une propriété remarquable, c’est que les deux entrées jumelles «ne se voient pas». Le coupleur est caractérisé par sa réjection entre les deux entrées jumelles.
Exemple d’applications :
- Couplage de deux générateurs pour appliquer deux signaux sur un récepteur, sans que les deux générateurs ne se perturbent.
- Couplage de deux émetteurs de fréquences différentes sur la même antenne. Mais le prix à payer, c’est une perte de 3 dB pour chaque émetteur. La puissance perdue est dissipée dans la résistance de 100Ω du coupleur.
Remarque 1 : on peut remplacer les lignes quart d’onde par des "pi quart d’onde" plus intéressants pour les fréquences basses. (voir en fin de ce chapitre)
Remarque 2 : il existe aussi d’autres coupleurs «3dB», qui fournissent des signaux non pas en phase, mais en quadrature. (voir aussi en fin de ce chapitre)
L’inconvénient du coupleur de wilkinson, c’est que la charge est symétrique, ce qui pose des problèmes pour les fortes puissances. Mais vous trouverez plus loin un symétriseur pouvant transformer cette charge symétrique en asymétrique 50Ω.
Coupleurs directifs.
La figure montre un exemple de coupleur directif : Le signal incident est appliqué sur une charge adaptée. Une partie de la puissance est induite dans la ligne couplée et disponible sur sa sortie ; Ici nous avons deux lignes peu couplées, et la puissance qui sort de la ligne couplée est faible (par exemple – 20 dB en dessous de la puissance incidente)
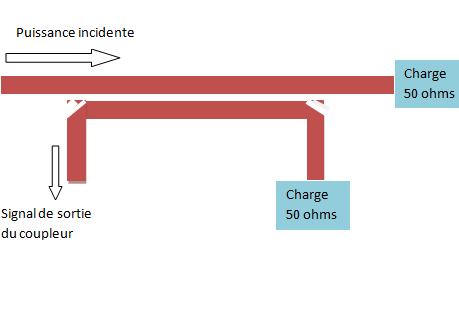
Ce type de coupleur permet de réaliser des réflectomètres, en plaçant deux lignes couplées de part et d’autres de la ligne principale, chacun dans un sens.
En effet, la ligne n’est couplée que pour l’énergie circulant dans un sens donné (celui des flèches sur la figure, donc qui montre le couplage dans le sens direct)...
Cette directivité est due au fait que dans un sens, les couplages E et H s’additionnent, dans l’autre ils s’annulent.
Mais là aussi, il peut y avoir des fuites : La « directivité » indique dans quelle mesure le signal qui doit être non couplé l’est quand même un peu.
Pour avoir des couplages supérieurs à -20 dB, il faudra des lignes couplées plus serrées, par différentes techniques (chevauchement ou entrelacement : coupleur de Lange) car deux pistes imprimées côte à côte dans le plan de la carte ne suffisent pas.
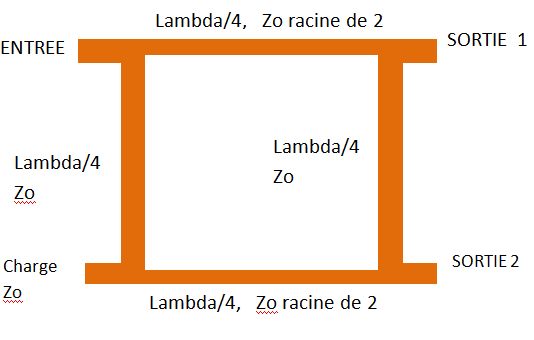
Le coupleur 90 degrés, 3 dB
Une autre application des lignes, ce coupleur possède deux sorties qui donnent chacune la moitié de la puissance appliquée à l’entrée. La sortie 2 est en retard de 90 degrés par rapport à la sortie 1.
La fréquence d’utilisation est donnée par la longueur des lignes quart d’onde.
En général, Zo = 50Ω, donc on a deux lignes quart d’onde d’impédance caractéristique 70Ω et les deux autres 50Ω.
La quatrième sortie "charge" recevra une puissance si les sorties 50Ω ne sont pas adaptées.
Remarque : "Le Pi quart d’onde" :
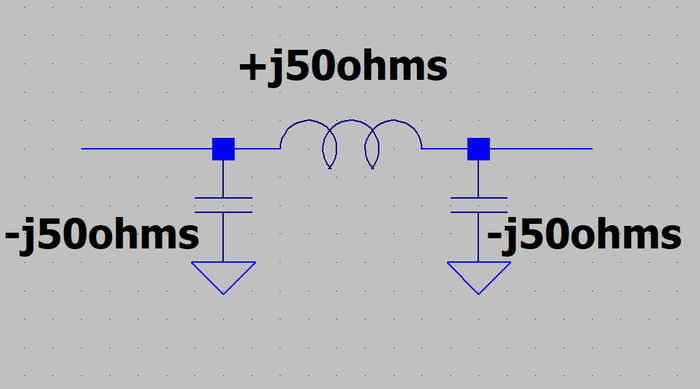
Une ligne quart d’onde d’impédance caractéristique Zc peut être remplacée par un circuit LC en pi équivalent :
capacité -jZc à la masse,
self série +jZc,
puis capacité -jZc à la masse.
Le schéma ci-contre montre un équivalent LC d’une ligne quart d’onde de Zc = 50Ω.
Attention, ce circuit est équivalent à la ligne quart d’onde seulement autour de la fréquence pour laquelle on aurait un quart d’onde, et pas sur les fréquences multiples ! (sur la fréquence double, un quart d’onde d’une vraie ligne devient une demi-onde...)
Ce circuit en pi particulier est parfois appelé "pi quart d’onde" et est utilisé pour réduire l’encombrement d’un circuit coupleur 90 degrés, ou d’un coupleur de Wilkinson vu plus haut.
Mais attention, aux fréquences élevées, les capacités de -j50Ω seront de valeur plus faible en pF, car la self parasite du boîtier et du via modifient la réactance.
Lignes utilisées en symétriseurs.
Il s’agit en fait de coupleurs particuliers. Par exemple, pour connecter un câble coaxial à une antenne qui présente une sortie symétrique, il faut utiliser un symétriseur, notamment pour éviter le courant de gaine dont nous avons parlé.
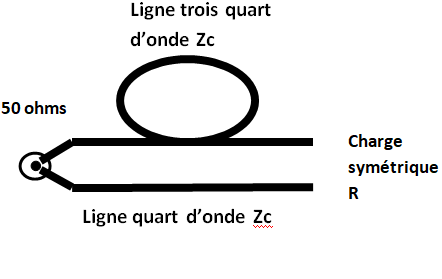
Astuce: Pour comprendre "comment ça marche", il suffit de savoir qu’une charge symétrique R est équivalente à deux résistances R/2 en série, avec leur point milieu à la masse.
Donnons un exemple de symétriseur transformant en 50Ω une charge symétrique R, utilisant deux tronçons de câble coaxial, un tronçon quart d’onde et un tronçon trois quart d’onde.
Si R = 50Ω, les deux tronçons de câble devront avoir une impédance caractéristique de 50Ω.
Si R = 100Ω, les deux tronçons auront Zc = 75Ω
Le coupleur en anneau
Nous avons vu que le coupleur de Wilkinson permettait de créer deux voies pour le signal, à partir d’une seule, ou inversement.
Mais la résistance 100Ω associée au coupleur de Wilkinson est symétrique (pas de borne à la masse). Nous pouvons transformer cette résistance symétrique en sortie asymétrique 50Ω, grâce au symétriseur vu ci-dessus.
L’association du coupleur de wilkinson (arc 1-2-3) et de ce symétriseur (arc 1-4-3) nous conduit au coupleur dit "en anneau". Pour des entrées /sorties 50Ω, la ligne constituant l’anneau aura une impédance caractéristique de 70Ω.
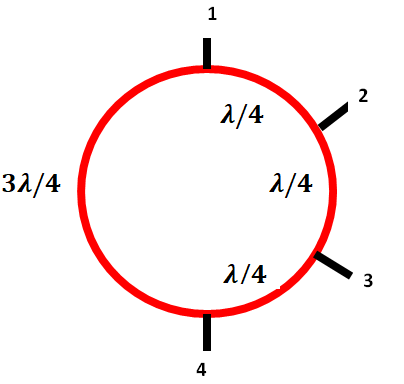
Le comportement est le même que pour un coupleur "0dB" de Wilkinson :
- Un signal appliqué en 2 est partagé en deux signaux (-3dB) en phase, sur 1 et 3.
- Deux signaux en phase appliqués sur 1 et 3 se retrouvent additionnés (+3dB) en 2.
- Deux signaux de fréquences différentes appliqués en 1 et 3 se retrouvent additionnés (-3db chacun) en 2 et aussi en 4.
Petite remarque : Ce type de coupleur peut être utilisé pour appliquer les sorties de deux émetteurs, de fréquences différentes, sur la même antenne.
Les émetteurs sont connectés en 1 et 3 et l’antenne est connectée en 2, où on retrouve les émissions additionnés. Le problème, c’est qu’on perd 3 dB de puissance.
On remarque qu’on trouve les puissances manquantes, additionnées en sortie 4.
Des petits malins vont se dire qu’on pourrait refaire la somme des signaux issus de 2 et 4, pour retrouver toute la puissance, ou bien appliquer ces signaux issus de 2 et 4, sur deux dipôles en phase de la même antenne, pour faire rayonner toute la
puissance.
Hélas, en faisant ceci, les signaux d’un des émetteurs se retrouveront en opposition.....On peut seulement utiliser la sortie 4 pour une autre antenne couvrant une zone différente, ce qu’on fait très bien pour les réseaux mobiles.