Couplage de circuits LC, filtre LC
Ce chapitre vous aidera à réaliser des filtres à circuits couplés LC.Lorsqu’on met en présence deux circuits LC ayant la même fréquence de résonance, il se produit un phénomène particulier :
à la résonance,l’énergie présente dans le premier circuit aura facilement tendance à atteindre le deuxième circuit.
C’est le phénomène de couplage. Par exemple, considérons deux circuits résonants identiques ayant chacun un Q=100.
Considérons le flux magnétique issu de la self du premier circuit. Si 1% seulement de ce flux entre dans la self du deuxième circuit,
on s’apercevra qu'à la fréquence de résonance, toute l’énergie du premier circuit sera transmise audeuxième !
En radiofréquences, ce qui nous intéresse ici, on utilise souvent des circuits couplés pour former des filtres.
Alors qu’un seul circuit LC présente une réponse du second ordre, deux circuits convenablement couplés permettront la réalisation
de filtres plus «abrupts», c'est-à-dire avec une réponse plate dans une bande désirée, et
une atténuation plus importante en dehors de la bande passante.

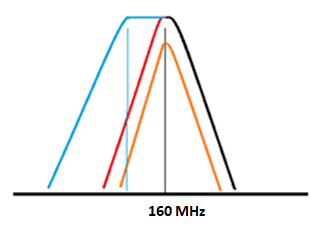
La courbe de réponse du filtre passe bande constitué de deux circuits identiques couplés accordés sur la même fréquence ressemble à ce que donne la figure ci-dessous. On voit que la forme de la réponse dépend du couplage.
Si les deux circuits sont faiblement couplés, la courbe de réponse sera étroite, mais toute l’énergie du premier circuit n’arrivera pas au second (courbe orange).
En augmentant le couplage, on atteint le «couplage critique»: toute l’énergie passe, on atteint un transfert maximum. (courbe rouge).
Si on continue d’augmenter le couplage, le sommet de la courbe de réponse s’élargit, (courbe bleue, pratiquement plate, avec une ondulation négligeable...)
Puis, si on augmentait encore le couplage, un creux de plus en plus profond apparaît au centre de la courbe de réponse. (non représenté sur la figure)
Facteur de forme:
Les systèmes de radiocommunications exigent très souvent une réponse "plate" dans une bande passante donnée, on définit ainsi une bande passante à -3dB. Mais ces systèmes exigent aussi un maximum d'atténuation en dehors de cette bande. On peut par exemple définir la bande en dehors de laquelle l'atténuation est supérieure à 20 dB.
On peut chiffrer la façon dont un filtre atténue les fréquences en dehors de sa bande passante, par le "facteur de forme" :
Un filtre composé d'uncircuit LC unique est un filtre du second ordre. Le rapport entre la bande à -20 dB et la bande à -3dB est de l'ordre de 10. On dit que le Le facteur de forme à -3dB/-20 dB est 10.
Pour un filtre composé de deux circuits LC couplés, à réponse "plate" (Au couplage critique, proche d'un filtre de Butterworth), le facteur de forme à -3dB/-20 dB est de 3 environ. On peut ameliorer un peu le facteur de forme en surcouplant, mais il faudra admettre un creux au centre de la bande passante. La forme se rapprochera alors de celle d'un filtre de Chebychev.
Si on désire des filtres encore plus performants, il sera nécessaire d'augmenter l'ordre du filtre, donc de multiplier le nombre de circuits LC. Le réseau deviendra alors plus complexe.
(Notons que pour les systèmes numériques, le filtrage du signal modulé ne nécessite pas forcément une bande passante plate, le temps de propagation des différentes fréquences dans la bande est plus critique. Nous n'aurons plus des filtres de type Butterworth, mais des filtres de Bessel ou des filtres gaussiens, par exemple.)
Comment coupler deux circuits ?
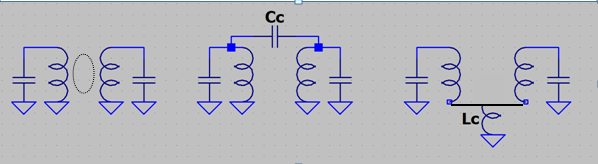
La figure ci-dessous montre les 3 façons les plus intéressantes pourcoupler deux circuits :
- Couplage par le flux magnétique.
- Le couplage par capacité en tête Cc.
- Le couplage par self en pied Lc.
Couplage critique :
C'est le couplage qui permet un transfert maximum d'énergie d'un circuit à l'autre, avec une bande passante à un seul sommet.
Il est important de connaître les règles qui permettent le couplage critique entre deux circuits identiques de même coefficient de surtension Q :
- Couplage par flux : il faut que le flux qui entre dans la bobine du deuxième circuit soit 1/Q fois le flux total de la première bobine.
- Couplage par capacité en tête : la capacité de couplage Cc est égale à la capa d'accord divisée par Q. (c'est donc une capacité relativement petite)
- Couplage par self en pied : la self commune est égale à la self d'accord divisée par Q. (donc une self relativement petite)
Surcouplage :
Nous avons vu que si on augmente le couplage au delà du couplage critique, la bande passante va s'élargir, mais un creux va se former au milieu de la courbe de réponse.
Remarquons que si on augmente le couplage en augmentant la capacité en tête ou en augmentant la self en pied, (voir plus haut les types de couplages) la bande passante s'étendra, vers les fréquences basses. Nous verrons que c'est utile pour la mise au point de telscircuits couplés...
Question : Y a-t-il d’autres couplages possibles ?
Oui, bien sur. Par exemple, on peut inverser L et C dans le couplage «self en pied» de façon que ce soient les capacités qui aboutissent à la self commune de couplage.
On peut aussi remplacer la "self en pied" de couplage par une "capacité en pied". Mais attention, comme cet élément de couplage en pied doit présenter une faible impédance, il faudra placer une capacité importante. Cela peut poser un problème en UHF, l'impédance faible de la capacité sera modifiée par la self constituée par son boîtier et sa piste de mise à la masse…
Quant au couplage par self en tête, il est rarement intéressant car il nécessite une self de grande valeur, qui présentera des capacités parasites.....
Si les résonateurs sontcomposés d’une ligne résonante, plutôt que d’une self et d’une inductance, on peut coupler deux lignes parallèles en les positionnant à une certaine distance l’une de l’autre. Il y aura à la fois couplage magnétique (champ H) et couplage électrique (champ E). Selon la disposition des lignes, ces deux couplages se renforceront ou pas. Voir le chapitre sur les lignes de transmission...
Un exemple de filtre avec deux circuits couplés.
Cet exemple montre la marche à suivre lors d'une simulation. Les résultats sont approchés, et la simulation permettra d'affiner les valeurs. Nous choisissons une fréquence assez basse pour n'avoir pas trop à se préoccuper des éléments parasites, mais le principe reste le même sur les fréquences plus hautes.
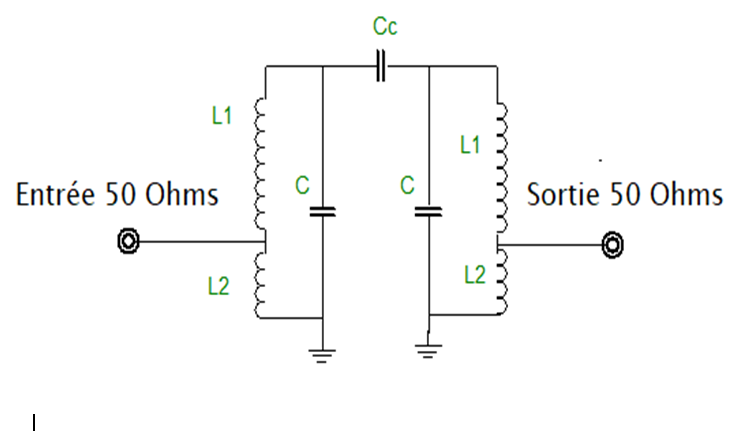
On se propose de construire un filtre passe bande centré sur Fo= 156 MHz, à l’aide de deux circuits LC couplés. On veut une bande passante de 8 MHz environ. L’entrée et la sortie seront en 50 Ω.
- Choisir le coefficient de surtension de chaque circuit:
On a choisi une bande passante à -3dB de 8 MHz pour le filtre complet.
Ce qui sera obtenu si chacun des circuits possède une bande passante du même ordre, soit :
Q = Fo/ Bande passante = 160 /8 = 20 - Quel type de couplage ?
Les deux couplages les plus courants sont le couplage par une petite self en pied et le couplage par une petite capacité en tête. Ces deux couplages permettent une mise au point facile, car ils ont une particularité: la fréquence de résonance de chacun des deux circuits AVANT couplage est égale à la limite haute de la bande passante.
Nous avons choisi ici le couplage par capacité en tête :
Connaissant le Q en charge des deux circuits et les capacités d’accord, nous en déduirons la capacité de couplage en tête qui donnera le couplage critique : Cc = Capacité d'accord /Q - L'accord de chaque circuit avant couplage :
Avec ce type de couplage, l'accord de chacun des deux circuits avant couplage devra se faire à la fréquence la plus haute de la bande passante, c'est à dire à F = 156 + 8/2 MHz = 160 MHz.
C'est cette fréquence qui va nous servir pour calculer les composants L et C des deux circuits AVANT couplage. - Choix des composants d'accord L et C :
Oublions pour l'instant le couplage, et définissons tout d’abord les impédances Z des selfs et capacités d’accord des deux circuits LC identiques.
En général, c’est un paramètre qu’on peut choisir. L’expérience pousse à choisir ces impédances ZL et Zc de l’ordre de la centaine d’Ω.
Si on choisit des impédances trop faibles (la dizaine d’Ω), on perdra en qualité du circuit LC (dégradation du coefficient Qo).
Si on choisit des impédances trop grandes (le millier d’Ω), on se heurtera à des problèmes de capacités parasites qui deviendront du même ordre que les capacités d’accord désirées.N'oublions pas qu'à la résonance, les modules de ZL et Zc sont égaux.
Choisissons donc ZL = j 100 Ω et Zc =-j 100 Ω.
À 160 MHz, le calcul donne une self de 100 nH et une capacité de 10 pF.
Nous supposerons que ces composants ont des pertes négligeables (Qo infini). Ce qui signifie que le Q sera donné uniquement par les charges.Vérifions le Qc de ces deux circuits. On a choisi la bande passante (à -3dB) de chaque circuit égale à 8 MHz, ce qui, par expérience, nous donnera aussi une bande passante de 8 MHz (mais plus plate) quand les deux circuits seront couplés.
Q = Fo/ Bande passante= 160 /8 = 20 .
Pour le couplage critique, la capacité de couplage sera donc :
Cc = C/Q = 10 pF /20 = 0,5 pF - Calcul de la résistance au point chaud :
Nous en déduisons la résistance fictive R au "point chaud" de chaque circuit :
R = QxZ = 20x100 donc R = 2000 Ω.(si vous ne suivez pas, revenez au circuit LC)
- Transformateur :
Décidons du type de transformateur d’impédance nous utiliserons, pour passer de R = 2000Ω au sommet, à 50Ω sur la prise intermédiaire.
Nous avons choisi sur le schéma de départle pont inductif.
La self d’accord est L totale = L1 + L2 = 100 nH (ce qu'on vient de voir)
On veut transformer en 50 Ω la résistance au point chaud R = 2000 Ω
Le rapport de transformation est donc de 2000/50 = 40
Le rapport des selfs : Ltotale / L2 est donc : √ de 40 = 6,3.
La self L2 fera 100nH / 6,3 donc L2 = 16 nH
La self L1 fera 100nH – 16 nH donc L1 = 84 nH.
Comment ça se passe en pratique, en simulation ou en circuits réels ?
En premier lieu, il faut trouver les accords exacts et précis de chacun des deux circuits LC avant couplage.
La méthode la plus simple est la suivante :
On réduit, provisoirement, fortement la capacité de couplage Cc de façon à être bien en dessous du couplage critique.
On a vu que pour le couplage critique, il faut Cc = 0,5 pF.
Nous ne placerons pour l'instant que Cc = 0,1 pF
De cette façon, l'accord de chacun des deux circuits n'influence pas l'autre, il correspondra, on vient de le voir, à 160 MHz, limite haute de la bande passante de l'ensemble couplé.
On règle donc les capacités d’accord de chacun des circuits pour obtenir le maximum de réponse sur la fréquence la plus haute de la bande passante désirée : Si nous voulons une bande de 8 MHz, centrée sur 156 MHz, on règlera les deux capacités d’accord pour un maximum vers le haut de la bande passante, donc à 160 MHz. On applique donc sur l’entrée un signal de 160 MHz, et cherche à obtenir le maximum en sortie du filtre en ajustant finement les deux capacités d'accord de chaque circuit. La réponse est très «pointue», puisque, avec Cc = 0,1 pF, nous sommes très en dessous du couplage critique…

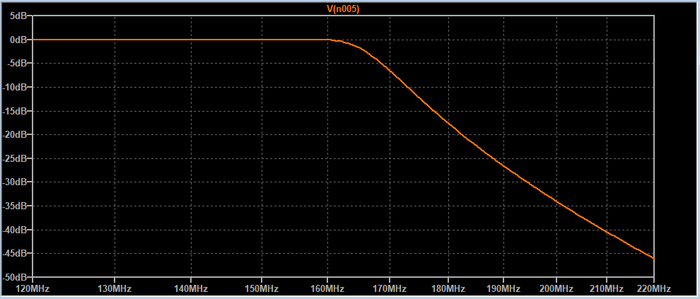
Ce résultat obtenu, on augmente la valeur de Cc. Comme nous n’étions pas encore au couplage critique, le niveau en sortie va augmenter jusqu'au couplage critique pour Cc = 0,5 pF… Figure ci-desssous.

Puis, en augmentant encore un peu Cc, on va constater que le niveau n’augmente plus, et que la courbe de réponse du filtre s’étale vers les fréquences basses.… Ce comportement est un des avantages du couplage par capacité en tête.
Avec Cc =0,70 pF la bande passante va s’étaler jusqu’à 152 MHz. Cette bande est presque plate, le creux central est de 0,5 dB.
Notons que si on augmentait encore Cc, la bande continuerait de s’étaler vers le bas, mais le creux central serait de plus en plus prononcé.
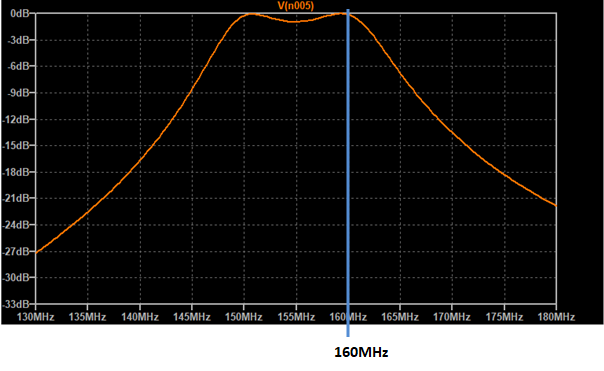
Pour fixer les idées, si la capacité de couplage est égale à 1,5 fois celle du couplage critique, le creux central reste inférieur à 1 dB et la bande passante à -1dB augmente de 50 % environ, par rapport à la bande passante du couplage critique.
Ajustage fin des valeurs
Bien sur, ces calculs théoriques ne tiennent pas compte des éléments parasites : capacité parasite des selfs, inductances parasites des capacités, pertes propres des selfs…toutes choses donc il conviendra de parler plus loin…
Les éléments parasites vont faire que les composants L et C ne seront pas tout à fait ceux calculés …
Les composants définitifs self et condensateur, seront un peu inférieurs en valeur, du fait que nous n’avons pas tenu compte des capacités parasites et des inductances parasites des pistes…
Et si on faisait un couplage par self en pied ?
On a vu que pour des Q élevés, la capacité de couplage est très petite...Elle le sera encore plus un UHF ou au delà... Ce qui peut poser des problèmes, il est difficile d'avoir des composants d'une fraction de pF ! On peut jouer sur la proximité de deux aplats de cuivre....
Une autre solution, c'est de coupler par une self en pied, de faible valeur. Des valeurs de selfs de l'ordre du nH sont envisageables, et même moins. Il s'agit simplement d'une piste très courte ...(en UHF, elle sera de l'ordre du mm, et en tenant compte de l'impédance du via de masse....)
Choisissons encore une fréquence 160 MHz,
un Q de 20,et des selfs d'accord L1 = L2 =100 nH.
L'impédance des selfs d'accord est toujours 100Ω, la résistance au point chaud est
R =100Ω x Q = 100Ω x20 = 2000Ω,
On aura le couplage critique lorsque la self de couplage sera L3 =L /Q = 100nH/20 = 5nH.

Maintenant, il faut présenter au générateur et à la charge des résistances de 50 Ω :
Pour changer de l'exemple précédent, nous allons faire une transformation à 50Ω non plus par pont inductif, mais par les capacités C3 et C4 (schéma ci-dessus).
Il reste à calculer ces capacité d'adaptation C3 et C4, pour transformer en 50Ω la résistance de 2000Ω du point chaud .
Si vous avez lu le Le circuit LC : l'impédance Z de C3 et C4 est telle que:
Z2 = ( résistance au point chaud) x R1 = 2000 x 50 = 100 000
d'où Z = 316 Ω ---> on prendra C3 = C4 = 3,2 pF (en pratique: 3,3pF ...)
La self doit s'accorder avec 10 pF, maisces capacités C3 et C4 comptent (au moins partiellement) dans la capacité d'accord... donc C1 et C2 feront moins de 10 pF.
Comme dans l'exemple précédent, on fera d'abord L3 bien inférieure au couplage critique, par exemple 1 nH (sous-couplage) .... On réglera alors les deux capas d'accord C1 et C2 pour avoir l'accord sur la limite haute de la bande passante: 160 MHz.
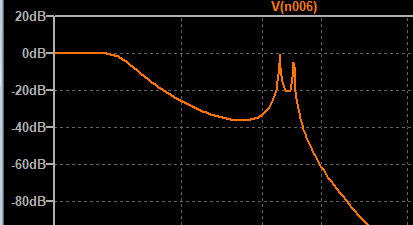
Ensuite on fera L3 = 5 nH pour obtenir le couplage critique.On obtient ainsi la courbe de réponse ci-contre ...La self de couplage L3 passée à 5 nHa pour effet d'étendre un peu la courbe vers les fréquences basses.
Si on augmente encore la self de couplage, la bande passante s'étalera encore plus vers les fréquences basses... Avec un creux central....

Nous avons aussi représenté le déphasage sur ce graphe. On voit que dans la bande passante, la phase varie de façon à peu près linéaire. Ce sera un paramètre important si le circuit filtre des signaux numériques..... La simulation consistera alors à optimiser les composants pour que la courbe de la phase soit proche d'une droite dans la bande passante à -3dB.
Et si on remplaçait la self de couplage en pied par un condensateur en pied ?
On peut même y trouver des avantages....En effet, si on s'intéresse à la réjection des fréquences loin de la bande passante, le mode de couplage a une importance. Ainsi, la couplage par capacité en tête , comme le couplage par self en pied, permettent une bonne réjection des fréquences basses . Par contre, si on veut augmenter la réjection hors bande des fréquences élevées, la capacité en pied sera plus intéressante.
Mais le couplage en pied demande une impédance faible, donc il faudra un condensateur de valeur assez grande: son impédance devra être Zself/ Q, soit dans l'exemple ci-dessus, pour le couplage critique, 100 /20 = 5 Ω. D'où une capacité de 200 pF.
En VHF (160 MHz ) un condensateur de 200 pF, c'est possible. Mais en UHF, un condensateur d'impédance faible posera le problème de sa self série. Lisez le Le condensateur réel pour vous en convaincre. Il faudra donc faire attention à ce problème....
Notons enfin que pour un couplage par condensateur en pied, la bande passante s'étale vers le haut quand on augmente le couplage, c'est à dire quand on diminue ce condensateur de couplage. Il faudra donc accorder les circuits avant couplage sur la fréquence la plus basse de la bande passante.
Et le couplage par flux ?
Parfois utilisé en plaçant deux circuits LC dans le même blindage. (filtres en "hélice" par exemple). Il est peu utilisé sur les cartes de conception professionnelle, car son modèle exige une description 3 D.
Utiliser des lignes à la place des circuits LC
Dans les bandes UHF ,un filtre LC bande étroite nécessite des éléments d'accord pour compenser l'imprécision des éléments L et C . Pour éviter ces éléments et pour avoir une bonne reproductibilité, on peut alors être tenté de remplacer les circuits LC par des lignes.
Un inconvénient des lignes, c'est la place ...Mais ce problème est souvent résolu en utilisant des résonateurs diélectrique quart d'onde à fort epsilon , que l'on trouve dans le commerce. Aini, un résonateur quart d'onde autour du GHz , avec epsilon = 40, aura une longueur réduite à 1,2 cm environ...
Ces résonateurs diélectrique sont très intéressants pour réaliser des filtres de bande entre 300 MHz et 3 Ghz...Ils ne nécessitent pas d'éléments de réglage et sont très stables.
Voici un exemple ci-dessous de filtre 950 MHz , de bande passante 20 MHz, sans réglage, sur plan de masse. Le schéma et la simulation sont sous SPICE. Vous trouverez aussi un exemple d'implantation, grille au pas de 1.27mm.
Nous avons couplé par capas en tête deux résonateurs quart d'onde 1 Ghz qui remplacent des circuits LC parallèle.
Les résonateurs de fréquence 1 GHz ont ici une impédance caractéristique standard de 8 ohms, et sont simulés par des lignes de Td = T/4 = 0,25 nS. Les capas C4 et C5 représentent la capacité des pads des soudures.
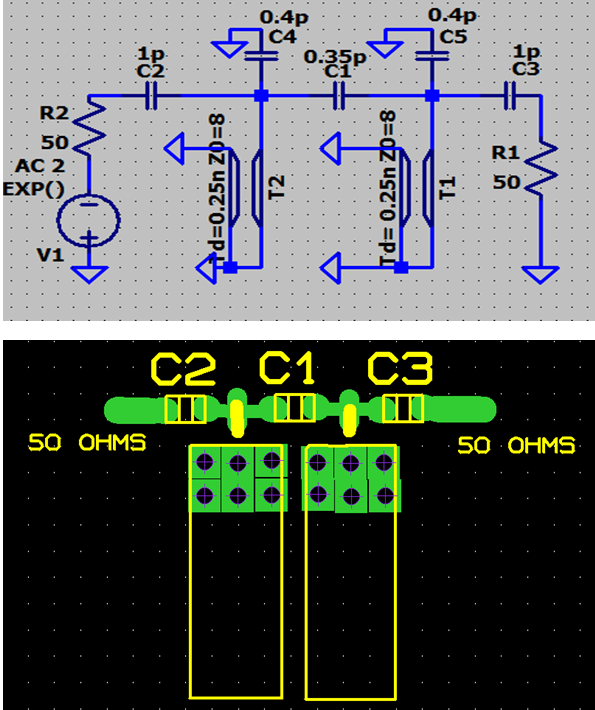
Voici la courbe de réponse . Attention, à cause des lignes , nous aurons aussi une réponse vers 2500 MHz, la fréquence triple. Pour éviter cette réponse, on fera suivre le filtre d'un petit circuit en pi passe bas de coupure vers 1 GHz.
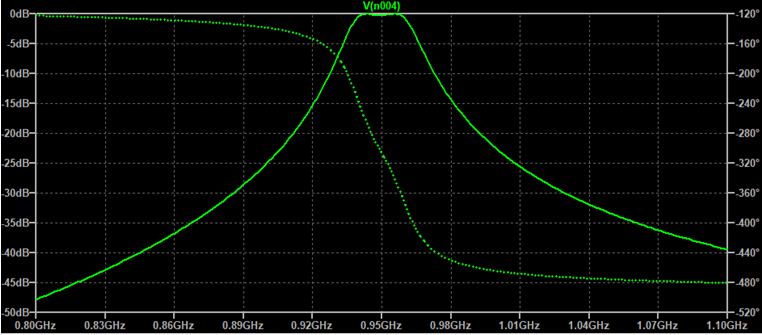
Et avec trois circuits résonants?
Il est possible de multiplier les circuits pour avoir un meilleur facteur de forme.
Par exemple, voyons comment faire avec trois circuits LC résonants, avec leschéma ci-dessous. On a conservé le couplage par capa en tête, et les valeurs :
Fo= 160 MHz,
C accord =10 pF (Zc = 100 Ω)
L accord = 100 nH
et Q = 20.
Cette fois, on a choisi (pour changer un peu) le générateur et la charge de résistance R de 2000Ω. Ils sont donc connectés directement aux points chauds des circuits, sans faire de transformation d'impédance..
Le Qc des circuits d'entrée et de sortie ainsi chargés est donc bien :
Qc = R /Zc = 2000 /100 = 20
Un couplage "critique" sera obtenu avec les capacités de couplage:
Cc = C3 = C4 =Caccord/2Q = 10pF/40 = 0.25 pF
On remarquera que la capacité d'accord du circuit central, est différente de celle des deux autres circuits, pour tenir compte des éléments de couplage.
Les adaptations entrée et sortie pourront aussi introduire une différence entre les capas d'accord du circuit central et celle des deux autres.
c'est intéressant à remarquer car la simulation d'un tel réseau introduit un degré de liberté de plus.

Pour la mise au point, plus délicate du fait qu'on a un degré de liberté supplémentaire :
- on conservera la symétrie entrée/sortie,
- on commencera avec les deux circuits d'extrémités.
- Ce n'est qu'ensuite qu'on introduira le circuit central, avec des couplages différents et un accord différent.
La mise au point se fera en choisissant un couplage critique pour réaliser le réglage fin (ici Cc= 0,25 pF).
On constate que le facteur de forme est bien meilleur qu'avec deux circuits, l'atténuation hors bande croissant plus vite.
Là aussi, les capas de couplage produisent un léger glissement vers les fréquences basses.
Remarque : Peut-on parler ici de "couplage critique ? La notion de couplage critique n'est pas la même qu'avec un réseau à deux circuits. Si le circuit central n'a pas de pertes, il existe une infinité de couplages critiques, en réduisant C4 et C5. En pratique, ce sont les pertes ( donc Qo) des circuitsqui limitent la sélectivité que l'on peut obtenir d'un tel réseau...
Quelques questions.
Question 1 : Comment régler le filtre si on n'a pas accès à sa sortie ?
Jusqu'ici, nous avons supposé qu'on injectait un signal sur l'entrée et qu'on analysait ce qui sortait. Mais si la sortie du filtre est inaccessible, par exemple connectée à un étage amplificateur à transistor ?
Pour les fréquences "coupées" par le filtre, l’énergie n’apparaît pas en sortie. Si le circuit lui-même ne dissipe pas (ou peu) l’énergie. Alors, si cette l’énergie ne « rentre » pas dans le filtre, elle ressort par son entrée. On dit qu’il y a « réflexion » des signaux sur l’entrée du filtre.
Il faut pour cela régler le filtre à l’aide d’un réflectomètre (coupleur directif). On règle le filtre de manière que l’énergie qui lui est appliquée dans sa bande passante soit bien absorbée par le filtre. De la bande de fréquence réfléchie, on peut déduire la bande transmise.
Par exemple, pour un filtre sans pertes dissipatives, une puissance réfléchie de -3 dB indique une puissance transmise à -3dB. (la moitié transmise, la moitié réfléchie..)
Attention, toutefois, cette méthode est peu précise si le filtre présente des pertes propres non négligeables.
Par ailleurs, notre exemple montre que le filtre attaque un amplificaeur. Il faudra que le niveau du générateur soit compatible avec le niveau d'entrée de l'amplificateur.
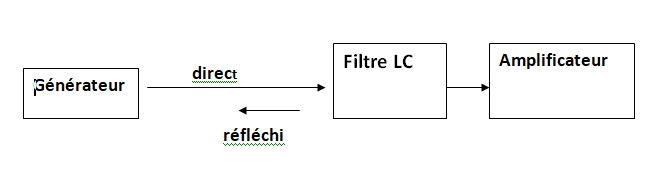
Question 2 : comment évaluer les pertes de transmission d’un tel filtre ?
Nous avons vu au "chapitre 2" que le coefficient de surtension Q d’un circuit LC est déterminé par deux causes d’amortissement : Les pertes propres du circuit, et l’amortissement par les charges connectées sur ce circuit.Dans l'exemple ci-dessus, nous avons supposé les composants parfaits, donc sans pertes : Qo infini .
Mais en pratique, le Qo n'est jamais infini, on peut représenter les pertes propres du circuit par une résistance de perte Ro en parallèle sur le circuit LC d'autant plus grande que Qo est grand.
L'amortissement du aux charges se représentepar une autres résistance R, en parallèle sur Ro.
Si Ro est très grand devant R, les pertes propres, dissipées par Ro, seront négligeables. Par contre, si par exemple Ro = R, alors la moitié de l’énergie injectée sur le circuit sera dissipée et manquera en sortie, et on aura une perte de 3dB pour chaque circuit.
Donc, un filtre présentera toujours plus ou moins de pertes dans la bande qu’il devrait passer. Pour minimiser ces pertes, il faudra que Ro soit grand devant R. ( Ou Qo grand devant Qc...)
En simulation, il suffira d'inclure dans le schéma les résistances de pertes (série) de chaque composant L et C ( voir chapitre 2)
Question 3 : L'ajustage fin est-il toujours nécessaire?
Si un filtre LC est très étroit, il est peu probable que les calculs ou la simulation donnent directement le schéma définitif. Ne serait-ce que du fait de l'imprécision des valeurs des composants.
Par contre, si les modèles sont corrects et prennent en compte tous les éléments parasites, il est possible de trouver directement les valeurs d'un réseau LC, si la bande passante est suffisamment large. Il faudra alors faire les calculs d'incertitudes en tenant compte de la précision de chaque composant.
Question 4 : Circuits résonants constitués de lignes?
Oui, c'est bien sur possible, mais c'est très encombrant en dessous du Ghz...Nous avons vu plus haut l'utilisation possible de résonateurs quart donde diélectriques .
D'autres exemples de couplages de lignes quart d'onde sont donnés dans le châpitre 3 "lignes de transmission".
Question 5 : Si je veux une plus grande réjection hors bande ?
Nous avons vu que le type de couplage entre circuits agit sur les atténuations loin de la bande passante. Par exemple, le couplage par capacité en tête est conseillé si on veut augmenter l'atténuation sur les fréquences basses. La capacité en pied des selfs, au contraire, atténue les fréquences hautes.
Lorsqu'on s'intéresse à l'atténuation proche de la bande passante, il faut s'intéresser au "facteur de forme", qui définit le rapport entre la bande passante à -3dB et la bande passante à -20 dB.
Par exemple. C'est "l'ordre" du filtre qui va jouer sur ce facteur de forme. Ainsi, un filtre "plat" proche d'un filtre de Butterworth, pourra donner une idée dufacteur de forme.
Si ce n'est pas suffisant, il faudra placer plus de deux circuits couplés. Nous avons vu un exemple à trois circuits LC. On peut multiplier le nombre de circuits à la suite. (filtres en échelle.) mais il faudra alors faire une étude théorique, car le nombre de degrés de liberté augmente, et il sera de plus en plus difficile à simuler sans passer par une étude théorique. Pour des entrées /sorties en 50 Ω, on cherchera à avoir une symétrie centrale. Si vous voulez atténuer une fréquence particulière, voyez le chapitre 15 sur les duplexeurs.
Question 6 : Peut-on placer plusieurs filtres l'un derrière l'autre pour obtenir de meilleurs facteurs de forme ?
Attention, les transferts en décibels de chaque circuit ne s'ajoutent pas nécessairement. Si, par exemple, sur une fréquence l'atténuation de chaque filtre est de 20 dB, le résultat ne sera pas forcément 40 dB si je place les deux filtres l'un derrière l'autre. En effet, l'atténuation hors bande passante d'un filtre est obtenue par une désadaptation. Pour comprendre ce qui se passe, supposons par exempleque la sortie du premier filtre, sur une fréquence hors de la bande passante désirée, soit une impédance R -JX. Si par hasard, l'entrée du filtre suivant est R +jX, la désadaptation disparaît et l'atténuation hors bande désirée aussi...
Pour que les courbes atténuations de deux filtres quelconques s'additionnent, on peut séparer les deux filtres par un amplificateur, de façon que les filtres ne se "voient" pas....
Heureusement, certaines configurations sont compatibles et peuvent gagner à êtremises l'une derrière l'autre. Par exemple, les cellules en pi passe-bas.. Ainsi, il est assez facile de créer sous 50Ω un filtre passe bas d'ordre élevé, de type Butterworh, constitué de plusieurs cellules LC en pi identiques.
Pour un filtre à une seule cellule, on a 0dB de pertes à la fréquence Fo à laquelle laself fait +j50Ω, encadrée par deux capacité de -j50Ω. On peut placer ces cellules en série. Plus on augmente le nombre de cellules, plus la forme devient "carrée" : Bande passante plate, et chute de plus en plus rapide hors de la bande. Pour plusieurs cellules, la fréquence de coupure à -3dB se situe assez loin de Fo, vers 1,35 Fo
Exemple, réseau en pi constitué de 4 cellules passe bas sous 50 Ω .
Il est intéressant de connaître les valeurs de L et C pour un filtre de fréquence de coupure à -3dB. Chaque cellule est constituée:
- d'une self de +j54 Ω,
- encadrée par deux capacités de -j28 Ω
Par exemple, pour une fréquence de coupure (à-3dB) Fc = 167 MHz :
- +j54 Ω ---> 51.5 nh
- -j28 Ω ----> 34pF
le réseau de 4 cellules donnera :

Nous aurons la réponse en fréquence ci-dessous :
- fréquence de coupure à -3 dB : 167 MHz
Jusqu'à 160 MHz, l'ondulation est inférieure à 0,2 dB.
Ce filtre pourra servir à atténuer les harmoniques d'un émetteur de fréquence maximale 160 MHz. (En tenant compte de la marge d'erreur sur les composants). L'atténuation de l'harmonique 2 ( 320 MHz) sera de l'ordre de 80 dB.
On pourrait aussi considérer non pas des cellules en PI, mais des cellules en T, que l'on placera de la même façon les unes à la suite des autres. Une simulation permettra d'affiner les valeurs, en partant ici aussi de selfs et de capas d'impédances 50Ω. Cependant, les cellules en Té demandent un plus grand nombre d'inductances, donc sont plus onéreuses...
Attention, ne mélangez pas les cellules en Pi et les cellules en Té, elles ne sont pas compatibles, vous aurez des remontées de niveau dans la bande à atténuer !
Attention encore. Une erreur à ne pas commettre lorsqu'on place plusieurs cellules les unes derrière les autres, c'est de grouper chaque cellule et les relier entre elles par un morceau de ligne 50 Ω, si court soit-il.
Dans ce cas, on observe en effet une réduction non désirée de l'atténuation dans la bande à atténuer comme indiqué ci-contre.
Et pour évaluer l'atténuation dans la bande passante ?
Pour minimiser les pertes, on choisira des inductances et des capacité à fort coefficient de surtension Qo.
Pour la simulation du filtre, on introduira la résistance de pertes en série avec l'inductance et la capacité. Si cette inductance présente une impédance j Z sur la fréquence considérée, alors la résistance de pertes série sera r = Z / Qo. Il suffira alors de placer cette résistance r en série avec l'inductance, dans le schéma utilisé pour la simulation....
Les couplages parasites...
Le couplage entre deux circuits n’est pas toujours un phénomène désiré.
Lorsque plusieurs circuits résonants sur la même fréquence sont à proximité l'un de l'autre, leur couplage va entraîner parfois de gros problèmes.
Par exemple, si le circuit en sortie d’un amplificateur réinjecte de l’énergie sur le circuit d’entrée, l’amplificateur pourra entrer en oscillation. (Ce qui arrive avec un transistor en émetteur commun, par la capacité base-collecteur)
On a vu que le couplage se fera d’autant plus que les Q sont élevés…
On peut réduire le couplage entre deux circuits LC:
- En évitant que le flux d’une self n’entre dans le flux de l’autre: Si les selfs sont proches, il sera difficile d'éviter un certain couplage. On croisera leurs axes .
- En évitant que les points haute impédance (points chauds) de chacun ne soient proches. En effet, si le Q est élevé, la moindre capacité entre ces points sera responsable d'un couplage par capacité en tête. C'est par exemple ce qui se passe dans un étage à transistor possédant un circuit LC en entrée et un circuit LC en sortie, la capacité base-collecteur (ou drain-source) pourra provoquer un couplage entre l'entrée et la sortie...
- En évitant que les courants qui circulent dans chaque circuit aient un chemin commun dans la masse dela carte: On évitera d'éloigner la masse de la self de la masse du condensateur de chaque circuit LC.
Pour éliminer le couplage entre deux circuits résonnants, on pourra enfermer chaque circuit dans un blindage. Ce blindage seraen aluminium, cuivre, laiton, etc...
L'épaisseur du blindage devra être de plusieurs fois l'"épaisseurs de peau"*, ce qui est toujours largement le cas en UHF. Le blindage élimine le couplage par flux, mais aussi par chemin commun dans la masse,
car les courants de masse ne circulent qu'à la surface intérieure du blindage. On pourra alors placer les blindages de deux circuits LC en contact entre eux sans qu'il y ait couplage.
Mais attention, le fait de mettre un blindage autour d’une self, réduira légèrement la valeur de l'inductance.
épaisseur de peau pour le cuivre : delta = 7µ @100 MHz et delta = 2µ @1 GHz